Izraz “dvojnica” je uporabil že Ptolemej, ki je tako opisal izgled Ni Strelca, dveh zvezd pete magnitude, ki sta na nebu oddaljeni le 14 ločnih minut (nekoliko manj od navideznega polmera Lune). Do srede 18. stoletja so odkrili še nekaj ducatov takih optičnih dvozvezdij. Menili so, da je bližina zvezd v vseh primerih le navidezna, saj zvezdi, ki sta daleč vsaksebi, zgolj slučajno vidimo v skoraj isti smeri.
Na možnost fizične povezave zvezd v dvojnicah je prvi pomislil John Mitchell, ki je leta 1767 objavil statistično analizo opazovanih razmikov dvojnic in ugotovil, da je bližnjih dvojnic mnogo več, kot bi jih pričakovali za primer naključnih poravnav. A odtod do sklepa, da taka fizična povezava zahteva medsebojno periodično gibanje obeh zvezd, je bilo še daleč.Občudovanja vredna je zato leta 1783 objavljena domneva tedaj komaj 18-letnega Angleža Johna Goodrickea, da je periodično spreminjanje sija zvezde Algol verjetno posledica “prekrivanja, ki ga povzroča veliko telo, gibajoče se okrog Algola.” Imel je prav, tako da je Algol prvi odkriti dvojni sistem, to je par zvezd, ki zaradi gravitacijske sile krožita okoli skupnega težišča. Goodricke je do smrti pri 22 letih odkril tudi periodičnost svetlobnih krivulj Bete Lire in Delte Kefeja. Astronomi tedanjega časa, zlasti sicer zelo zaslužni Sir William Herschell, Goodrickeve razlage niso takoj sprejeli. Binarna razlaga sprememb Algola in drugih kratkoperiodičnih dvojnic je bila dokončno sprejeta šele pred sto leti, ko so opazili enako periodo tudi v Dopplerjevih premikih spektralnih črt.
Umetnikova upodobitev naših predstav o kataklizmični spremenljivki.
V veliki večini primerov so orbitalne periode daljše od enega leta, zvezdi pa zato dovolj daleč narazen, da se ne “motita”. Videz in razvoj takih zvezd je zelo podoben kot pri samostojnih zvezdah, ki nimajo spremljevalca. Dejstvo, da sta taki zvezdi vezani v dvojni sistem, je zanimivo predvsem zato, ker je v posebnih primerih mogoče izmeriti masi obeh zvezd. Masa zvezde, ki je ne znamo izmeriti na noben drug način, je osnoven parameter, ki določa njeno razvojno pot. Zato so opazovanja takih dolgoperiodičnih sistemov pomembna za preverjanje teoretičnih predpostavk o strukturi in razvoju zvezd.
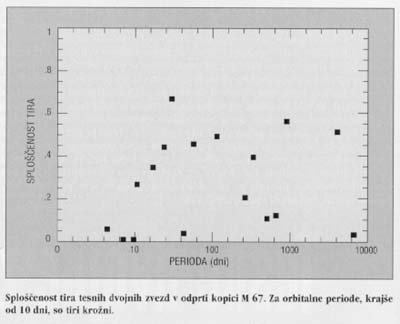
V tem sestavku se bomo zanimali le za zvezde, ki so blizu skupaj, torej za take z orbitalno periodo, krajšo od enega dneva. Plimska sila zaradi navzočnosti spremljevalca povzroči, da zvezda v takem sistemu ni več povsem okrogla. Če je tirnica sploščena ali če zvezda ne gleda svojega spremljevalca vedno z isto stranjo (okrog lastne osi se zavrti hitreje ali počasneje, kot naredi en obhod), tako “gnetenje” zvezdi neprestano spreminja obliko. Pojav je podoben plimskim valovom na Zemlji, ki neprestano spreminjajo obliko površine oceanov (pa tudi Zemeljske skorje). Zaradi trenja taka zvezda troši energijo in sčasoma preide v energijsko najugodnejšo konfiguracijo, to je krožno orbito z vrtilnim časom, enakim obhodnemu. Podrobnosti tega procesa še ne razumemo povsem, vendar opazovanja opravičujejo privzetek, da so tiri vseh tesnih dvojnic krožni ter da se vrtilni časi ne razlikujejo preveč od obhodnih.
Kljub krožnemu tiru in korotaciji vpliv spremljevalca ostane. Če je zvezda dovolj velika v primerjavi z razdaljo do spremljevalca, ima njena površina obliko tako imenovanega Rochovega ovala z “nosom”, ki gleda proti spremljevalcu. Snov na koncu nosu ni več gravitacijsko vezana na zvezdo, ampak pada proti spremljevalcu. V takem dvojnem sistemu se torej snov pretaka z ene zvezde na drugo. Rochov oval predstavlja zgornjo mejo za velikost kakršne koli zvezde v dvojnem sistemu, saj je za snov zunaj Rochovega ovala energijsko ugodneje, da odteče proti spremljevalcu. Kot smo omenili zgoraj, je masa ena najpomembnejših količin, ki določa razvojno pot zvezde. Masni pretok lahko zato zelo spremeni razvoj zvezd v tesnih dvojnih sistemih. Posledice so včasih drastične: zvezda, ki maso izgublja, lahko povsem izhlapi, zvezda, ki maso dobiva, pa lahko eksplodira v izbruhu supernove.
Kataklizmične spremenljivke
Zaradi obširnosti teme moramo naše zanimanje še bolj omejiti: govorili bomo le o dvojnih sistemih, v katerih je zvezda, ki maso dobiva, bela pritlikavka. Takim dvojnim sistemom pravimo kataklizmične spremenljivke. Vsega poznamo 751 takih dvojnih zvezd. Naše razglabljanje bo v glavnem veljalo tudi za rentgentske dvojnice, ki se razlikujejo le v tem, da vsebujejo namesto bele pritlikavke nevtronsko zvezdo ali črno luknjo. Bela pritlikavka je kompaktna zvezda, približno Sončeve mase, velika pa je le toliko kot Zemlja. Predstavlja zaključek razvoja zvezd, podobnih Soncu.
Površina zvezde je (če zanemarimo Coriolisove sile) ploskev konstantne vsote gravitacijskega in centrifugalnega potenciala. Prostornina zvezde, katere površinske plasti odtekajo proti spremljevalcu, je sorazmerna z maso zvezde. Tako je povprečna gostota take zvezde neodvisna od njene mase. Izračunamo jo lahko že, če poznamo orbitalno periodo dvojnega sistema. Če poznamo zvezo med velikostjo in maso zvezde, ki izhaja iz njene notranje strukture (za zvezde, v katerih gori vodik in so lažje od Sonca, je masa sorazmerna s polmerom zvezde), lahko iz znane gostote izračunamo maso zvezde v odvisnosti od orbitalne periode. Kataklizmične spremenljivke imajo orbitalne periode med eno in 10 urami, kar ustreza zvezdam donorjem z masami med desetino in eno Sončevo maso. Tako smo prišli do pomembnega spoznanja, da so dobri kandidati za zvezde, ki v kataklizmičnih spremenljivkah izgubljajo maso, prav lahke zvezde, v katerih gori vodik. Ker je teh zvezd v Galaksiji obilo, verjamemo, da so takega tipa donorji v vseh kataklizmičnih spremenljivkah.
Snov, ki jo izgublja donorska zvezda, začne padati proti kompaktnemu spremljevalcu, vendar ga ne zadene. Položaj je podoben kot pri kepanju na vrtiljaku: če vržemo snežno kepo v soseda na nasprotnem stolu, ga bomo zgrešili. Snov zaokroži okrog kompaktne zvezde in se nabere v akrecijskem disku, ki obkroža kompaktno zvezdo. Disk je tenek in če proti kompaktni zvezdi padajoče snovi ni preveč, se gibljejo posamezni delci v disku skoraj neodvisno, kot nekakšni mikroskopski planeti okoli sonca. Snov v disku se vrti, vendar ne tako, kot se vrti krožnik, to je kot togo telo. Keplerjev zakon nam pove, da krožijo kompaktni zvezdi bližji deli diska hitreje od bolj oddaljenih. Zaradi nastalega trenja se delci polagoma selijo vedno bliže kompaktni zvezdi in končno tudi padejo nanjo.
Tak disk je zelo svetel. Pa ne zaradi trenja med delci, ampak zato, ker so delci v notranjih delih diska mnogo bolj gravitacijsko vezani od tistih na zunanjem robu. Delec, ki tako drsi v globok potencialni “lonec”, porabi polovico sproščene potencialne energije za povečanje kinetične energije, ki se kaže kot vedno večja hitrost kroženja. Preostalo polovico mora izsevati. Groba ocena pokaže, da pri padanju na belo pritlikavko izseva vsak kilogram snovi preko 1012 J, pri nevtronski zvezdi pa celo do 1016 J. To je veliko celo za astronomske razmere, saj se pri energijsko najbolj izdatni jedrski reakciji, zlivanju vodika v helij v sredicah zvezd, sprosti “le” 7*1014 J na kilogram snovi. S pretokom mase proti kompaktnemu objektu skušamo zato razložiti najsvetlejše objekte v vesolju, kot so kvazarji in druge aktivne galaksije. Večina energije se izseva v obliki svetlobe kratkih valovnih dolžin, zato so tovrstni objekti bolj modri od objektov v svoji okolici.
Posledice masnega pretoka
Skoraj vedno se vsa masa, ki teče z zvezde, končno usede na kompaktno spremljevalko. Tako masa zvezde polagoma pada, masa bele pritlikavke pa raste. Spreminjajo pa se tudi razsežnosti dvojnega sistema. Poleg mase sistema, to je vsote mas obeh zvezd, se zdi smiselna domneva, da se ohranja tudi celotna vrtilna količina, saj je sistem izoliran od okolice. Levji delež vrtilne količine je shranjen v tirnih vrtilnih količinah obeh zvezd. Kompaktna zvezda je majhna, zvezda, ki maso izgublja, pa ima večino snovi blizu središča. Ob vrtilnem času, ki je enak obhodnemu, lahko zaradi mnogo manjše ročice spinsko vrtilno količino vrtenja zvezd okrog lastne osi zanemarimo. Račun pokaže, da je razdalja med središčema zvezd sorazmerna s kvadratom razmerja vrtilne količine in produkta mas obeh zvezd. Ob stalni vrtilni količini in vsoti mas obeh zvezd se tako razdalja med zvezdama manjša, če je zvezda donor masivnejša od kompaktne zvezde. Če pa je donor manj masivna komponenta sistema, zvezdi lezeta narazen. To je enostavno razložiti tudi z besedami, saj v zadnjem primeru prenašamo maso bliže težišču sistema in se mora za ohranitev vrtilne količine ročica oziroma razdalja zvezde donorja povečati.
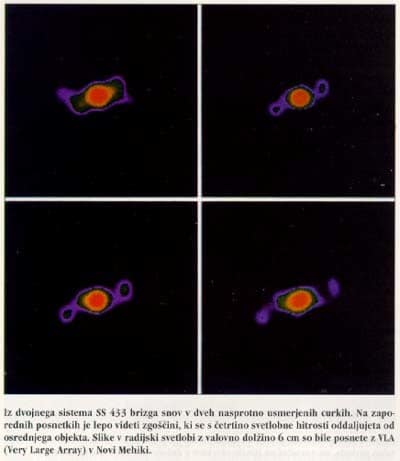
Če je zvezda, ki izgublja maso, težja od spremljevalke, se velikost dvojnega sistema začne manjšati. To močno pospeši pretok mase. Manjšanje prostornine Rochovega ovala je tako hitro, da se zvezda ne more dovolj hitro krčiti. Posledica je katastrofalno hitro izgubljanje mase, ki je je toliko, da se ne more vsa sproti usesti na kompaktno spremljevalko. Primer takega dogajanja je eden najsvetlejših objektov v naši Galaksiji, dvojni sistem SS 433. Da je dogajanje res burno, dokazujeta dva curka, v katerih snov s četrtino svetlobne hitrosti zapušča okolico kompaktnega objekta. Takih objektov ni veliko, zato pretok mase od bolj masivne zvezde k lažji ne more biti tipičen za tesne dvojnice. Razlog je v tem, da se ob tako močnem pretakanju masi zvezd hitro izenačita, sistem začne lesti zopet narazen, prenehanje krčenja prostornine Rochovega ovala pa povzroči tudi zmanjšanje masnega toka.
Pravzaprav se moramo vprašati, kaj sploh vzdržuje pretok mase od manj masivne zvezde k masivnejši spremljevalki. Kot smo razložili zgoraj, je masni pretok posledica dejstva, da zvezda napolnjuje svoj Rochov oval in tako izgublja površinske plasti. Z večanjem razdalje med zvezdama mora velikost Rochovega ovala rasti. Torej se mora za ohranjanje masnega pretoka napihovati tudi zvezda. Vendar se to ne zgodi, saj so v kataklizmičnih spremenljivkah zvezde, ki izgubljajo maso, lažje od Sonca. Celotno strukturo, in s tem velikost takih zvezd, določa gorenje vodika v njihovih sredicah. Goriva pri takih zvezdah zlepa ne zmanjka, okoliščina, da je taka zvezda v dvojnem sistemu, pa na sredico v ničemer ne vpliva. Zato se take zvezde ne razširijo.
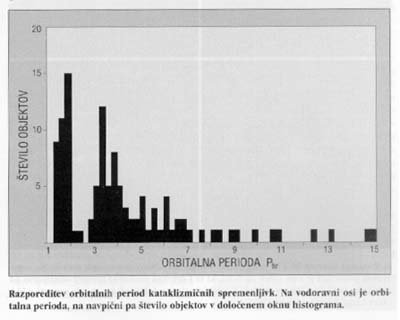
Ali torej domnevno širjenje Rochovega ovala prekine masni pretok? Zdi se, da ne. V zgornjem razglabljanju smo namreč tiho privzeli, da se vrtilna količina sistema ohranja. Je mogoče, da bi se manjšala? V tem primeru se Rochov oval ne bi širil in izpolnjeni bi bili vsi pogoji za dolgotrajen masni pretok. Diagram razporeditve orbitalnih period kataklizmičnih spremenljivk kaže veliko podrobnosti in nihanj, ki niso le posledica majhnega števila opazovanih objektov. To posredno podpira obstoj dolgotrajne faze masnega pretoka z znatnimi spremembami vrtilne količine sistema, saj je le težko razumeti, da bi imele dvojnice tako razporeditev orbitalnih period že ob samem nastanku.
Mehanizma manjšanja vrtilne količine sicer izoliranega dvojnega sistema še ne razumemo povsem. Za orbitalne periode krajše od treh ur sta zvezdi dovolj blizu, da tak sistem seva gravitacijske valove in se mu zato vrtilna količina manjša. Žal ta elegantna rešitev ne pride v poštev za periode nad tremi urami, saj je sevanje gravitacijskih valov prešibko. Najbolj upoštevana alternativa je tako imenovano magnetno zaviranje. Mehanizem so prvič uporabili za razlago relativno počasnega vrtenja Sonca. Sončevo magnetno polje sili delce v sončnem vetru, da korotirajo s Sončevim vrtenjem še, ko so že sto Sončevih polmerov daleč. Ko se vplivu polja končno iztrgajo, imajo ti delci zaradi velike ročice zelo veliko specifično vrtilno količino. Sonce se polagoma ustavlja, podobno kot drsalka, ki pri pirueti razširi roke. Verjamemo, da se na podoben način izgublja tudi vrtilna količina v dvojnem sistemu, če le ima donorska zvezda dovolj močno magnetno polje in zvezdni veter.
Razvoj: od kod in kam
Do sedaj smo govorili o kataklizmičnih spremenljivkah kot o homogeni skupini objektov. V resnici se po opazljivih lastnostih dokaj razlikujejo. V sistemih tipa AM Herkula, na primer, snov sicer teče proti beli pritlikavki, ki pa ima tako močno magnetno polje, da prepreči nastanek akrecijskega diska. Za številne objekte, še posebej nove, so značilni močni izbruhi, ki so posledica jedrskega zlivanja na površini bele pritlikavke.
Razvojno sliko moramo seveda graditi na skupnih značilnostih kataklizmičnih spremenljivk: to so dvojni sistemi s kratko orbitalno periodo in masnim pretokom na belo pritlikavko. Kam se torej razvije kataklizmična spremenljivka? Kot smo videli zgoraj, se mora za vzdrževanje masnega toka manjšati vrtilna količina sistema. Večino dvojnih sistemov doleti miren konec: ko se prenese dovolj mase, se struktura donorske zvezde dovolj spremeni, da zvezdni veter presahne, magnetno zaviranje preneha zmanjševati vrtilno količino, tako da se ustavi tudi masni tok. Preostali par zvezde z majhno maso in bele pritlikavke je brez masnega toka tako temen, da ga le stežka opazimo. Možen pa je tudi drugačen konec: če na belo pritlikavko priteče dovolj snovi, lahko bela pritlikavka postane nestabilna, eksplodira in nastane supernova. (Pritekajoča snov ne sme vsebovati vodika, sicer se ta začne spajati v helij in dobimo novo.)

O nastanku kataklizmičnih spremenljivk ne vemo kaj dosti. Navzočnost bele pritlikavke, ki je končna faza razvoja zvezd, podobnih Soncu, sicer zagotovo govori o tem, da se je snov med zvezdama pretakala že tudi v preteklosti. Žal pa ne vemo odgovora na osrednjo dilemo: tako teoretična razmišljanja kot opazovanja kažejo, da je razdalja med zvezdama ob nastanku dvojnega sistema zelo velika, tipično več tisoč zvezdnih polmerov. Mehanizma, ki lahko skrči tako razsežno orbito na le nekaj zvezdnih polmerov veliko orbito kataklizmične spremenljivke, še ne poznamo.
Situacija je nekoliko podobna težavam Johna Mitchella s prevelikim številom bližnjih dvojnic. Le Goodricke se, kot kaže, še ni rodil.
Tomaž Zwitter, ponatis članka iz revije Spika (februar 1994)
















