|
Kako se lahko neskončno veolje še naprej širi? Saj se vendar nima več kam širiti?! Tako ali tako je neskončno in svoje velikosti ne more več povečevati… |
kvarkadabra.net |
Razmisli o naslednjem: naravnih števil je neskončno. Sedaj naravnim številom dodaj ničlo. Vsakemu številu prištej nato enico: iz ničle tako nastane enica, iz enice dvojka in tako naprej. Splošno : n’=n+1. Zopet dobiš (samo) vsa naravna števila. Je sedaj, po tem, ko smo dodali enico in na novo prešteli novo množico, naravnih števil več ali manj kot prej (na začetku smo vendarle dodali ničlo, kajne)?
No vidiš, to je primer operacije na neskončni množici (v tem primeru števno neskončni množici), ki je morda nekoliko kontraintuitivna. Iz običajnega življenja smo pač navajeni operacij s končnimi množicami- če desetim jabolkom dodamo še eno je teh pač enajst. V gornjem primeru pa je obeh števil “enako neskončno”. Kar smo naredili, bolj učeno imenujemo bijektivna preslikava med dvema števno neskončnima množicama.
O končnosti in neskončnosti vesolja pa: obstaja tudi model vesolja, ki je končen. Čeprav se sedanja opazovanja bolj nagibajo k neskončnemu modelu vesolja ( ki je ravno in ima kozmološko konstanto), pa takšno zaprto vesolje ni povsem izključeno. Če je vesolje zaprto, je namreč končno, torej ne neskončno!
Seveda pa nima meje. Tako kot npr. dvodimenzionalna ploskev balona. Zamisli si, da si mravlja, ki lahko hodi le po površini balona. Zate je svet dvodimenzionalen in ne tridimenzionalen. Pa naj se mravlja odpravi na sprehod, pri čemer vedno hodi le naravnost naprej, brez zavijanja. Če bo hodila dovolj dolgo, se bo vrnila nazaj na mesto s katerega je sprehod začela. Ko bo pač prehodila celoten obseg balona. Ker tak sprehod lahko naredi v vsako smer iz poljubne točke na balonu, je to dokaz dveh stvari: njen svet je končen (bolj natančno: njegov dvodimenzionalen volumen (površina) je končen) in tudi nima roba (nikjer na sprehodu se mravlja ni zaletela v rob balona, mejo preko katere ne bi mogla).
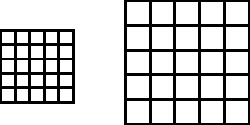
Ko se mravljino vesolje-balon širi, se mu povečuje polmer. Tako nekako (a samo približno), kot da bi napihovali balon. V primeru neskončnega vesolja se povečuje karakteristična skala. To pomeni, da se razdalja med dvema v prostoru mirujočima točkama sčasoma povečuje. Vse skupaj si zlahka ponazorimo na primeru mreže. Zamislimo si, da v dvodimenzionalnem vesolju označimo razdalje v nekem trenutku z mrežo. Ko se vesolje širi, se velikost mreže povečuje in s tem tudi karakteristična skala – karakteristična skala je tu na primer lahko kar velikost enega okenca v mreži.
Ko se vesolje širi, se povečuje karakteristična skala- razdalja med v prostoru mirujočimi objekti.
Seveda pa še vedno vesolje ostaja končno, če je bilo na začetku končno (zaprto vesolje) oziroma neskončno, če je bilo na začetku neskončno (odprto vesolje). Primer neskončnega vesolja je na primer vesolje z negativno ukrivljenostjo- predstavnik take površine je sedlasta struktura z negativno ukrivljenostjo. Drug primer neskončnega vesolja pa je ravno vesolje, kjer je ukrivljenost seveda enaka nič.
Pomembno pri tem je, da neskončno vesolje ravno tako kot končno (balon) nima roba. To pomeni, da se lahko širi, ob tem pa ničesar ne odrinja- saj vendar ni roba za katerim bi se vesolje kar nenadoma končalo.
Ob tem se vrnimo še za trenutek nazaj k mravljinemu dvodimenzinalnemu vesolju- balonu. Le to je vloženo v tridimenzionalni prostor. Seveda, le pretvarjali smo se, da je balon dvodimenzionalen objekt, prav tako tudi mravlja. Dvodimenzionalen je le v toliko, v kolikor lahko pozabimo na debelino gume balona in na višino mravlje. Poleg tega bi morali pozabiti tudi na okolišnji 3D prostor. Če naj bo to pravo vesolje z eno časovno in dvema prostorskima dimenzijama, moramo namreč odmisliti sliko, kjer je le to vloženo v naš običajni prostor s tremi prostorskimi in eno časovno dimenzijo. Tako pravo dvodimenzionalno vesolje je svet povsem zase, brez kakršnekoli povezave z našim tridimenzionalnim prostorom. Torej tudi širjenje dvodimenzionalnega vesolja ne bo pomenilo nekega napihovanja npr. balona v večjem 3D svetu. Vesolje je pač svet zase in ni vloženo v nek “večji” prostor.
Sedaj seveda pride še težji korak. V primeru balona smo si zlahka predstavljali ukrivljenosti in napihovanje balona. Sedaj pa si moramo iz 2D površine balona zamisliti 3D površino neke namišljene štiridimenzionalne sfere, nato pa pozabiti na to, da je naša prispodoba slike vesolja ob danem trenutku vložena v štiridimenzionalni evklidski prostor. Poleg tega se ta 3D površina še sčasoma napihuje. To je sedaj slika realističnega zaprtega modela vesolja. Če je vesolje odprto (in s tem neskončno), pa imamo po drugi strani ali opravka s 3D ploskvijo s konstantno negativno ukrivljenostjo, kar nas odpelje še nekoliko dlje od zmožnosti nazornih predstav, ali pa je to navaden raven prostor (ukrivljenost je enaka nič).
Glej še
O standardnem in stacionarnem modelu vesolja
Česa je v vesolju več – mase ali energije?
Zelo kratka zgodovina časa na Kvarkadabri
O vesolju na Kvarkadabri
Kaj je bilo pred prapokom?
Ali točka v središču vesolja miruje?