Težave z interpretacijo kvantne fizike

V članku poskušamo opredeliti bistvene posebnosti kvantnega sveta (superpozicija stanj, kvantna prepletenost…), ki jih v okviru klasične fizike ne moremo pojasniti. Formuliramo tudi problem meritve kot nujno posledico ortodoksne (Dirac – von Neumannove) interpretacije kvantne mehanike in linearnosti kvantne dinamike ter predstavimo nekaj aktualnih predlogov za njegovo razrešitev.

Kvantna mehanika je fizikalna teorija, ki opisuje in napoveduje obnašanje submikroskopskih sistemov kot so npr. atomi in elektroni. Danes velja – poleg splošne teorije relativnosti – za eno najbolj uspešnih orodij obravnave in napovedovanja dogajanja v naravi. Čeprav ji po kriteriju funkcionalnosti ni kaj oporekati, so z njeno interpretacijo še vedno težave. Svet kvantne mehanike se po svojem obnašanju namreč bistveno razlikuje od našega vsakdanjega sveta, čeprav je makrosvet predmetov, ki nas obkrožajo, tudi sestavljen iz atomov in podobnih kvantnih delcev, za katere veljajo pravila kvantnega sveta. Ameriški fizik Richard Feynman, ki je za svoj prispevek h kvantni teoriji prejel Nobelovo nagrado, je večkrat poskušal predstaviti čudnost kvantnega sveta širši publiki, ki ni ravno vešča višje matematike. V predavanju na Cornell University je leta 1964 razlagal:

“Elektroni v atomu se ne obnašajo kot uteži, ki visijo na vzmeteh; tudi ne kot mali sončni sistemi z majhnimi planeti, ki krožijo okoli jedra v orbitah. Elektroni tudi niso nekakšni oblaki megle, ki obkrožajo atomsko jedro; pravzaprav jih ne moremo primerjati z ničemer, kar smo že kdaj videli! Vseeno pa je nekaj, kar nam olajša njihovo obravnavo: elektroni se v določenem oziru obnašajo povsem enako kot fotoni, kar pomeni, da so oboji malo prismojeni, a oboji povsem na enak način.”

Preden se lotimo problemov, ki so povezani z interpretacijami dogajanja v kvantnem svetu, si poskušajmo najprej razjasniti, kaj je v opisu kvantnega sveta sploh tako drugačno od tega, kar smo navajeni iz vsakdanjega sveta. Če bi fizike vprašali, po čem se kvantna mehanika bistveno razlikuje od klasične mehanike, bi se odgovori verjetno vrteli okoli dveh ugotovitev:

• kvantni sistemi nikoli nimajo hkrati točno določenih vrednosti vseh svojih dinamičnih spremenljivk in
• kvantni sistemi so lahko v “superpoziciji” oz. v več različnih stanjih hkrati.

Različne interpretacije kvantne mehanike so predvsem poskusi, kako razumeti ti dve posebnosti kvantnega sveta.

Superpozicija kvantnih stanj

Oglejmo si primer elektrona, preprostega kvantnega delca, katerega ena od lastnosti je, da ima spin 1/2¹. Kaj točno to pomeni, za nas ne bo pomembno. Dovolj bo, če vemo, da vedno, ko spin elektrona izmerimo v katerikoli smeri, dobimo le enega od dveh možnih odgovorov: spin elektrona je obrnjen ali naprej ali nazaj v smeri merjenja. Nas bo zanimala predvsem vrednost spina v navpični smeri (x-spin). Da bi si čim lažje predstavljali, kaj se dogaja v kvantnem svetu, si spin preprosto predstavljamo kot “običajno” lastnost delca, podobno kot ima makroskopski predmet npr. določeno barvo. Po analogiji z objekti makrosveta si zamislimo spin gor, kot da je delec zelen, spin dol pa, kot da delec ni zelen. To sta v običajnem svetu dve izključujoči lastnosti. Intuitivno bi tako lahko po analogiji sklepali, da ima elektron v določenem trenutku spin le navzgor ali pa navzdol, nikakor pa ne oboje hkrati, saj bi to v prenesem pomenu besede pomenilo, da je zelen in ne-zelen hkrati. Vendar pa naša intuitivna predstava za kvantne delce ne drži povsem. So situacije, ko elektron (poimenujmo ga S kot sistem) nima določene vrednosti spina v izbrani smeri. V takšnem primeru je S v stanju, ki ga imenujemo superpozicija stanj. Elektron je tako hkrati zelen in ne-zelen, česar si seveda ne moremo prav dobro predstavljati.

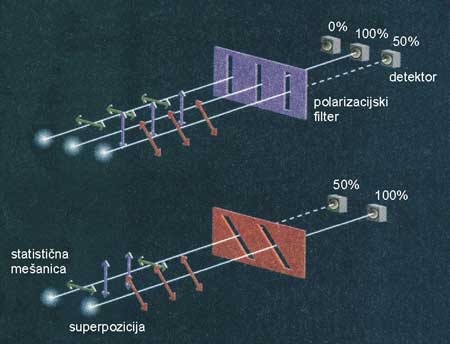
Da si pojem superpozicije stanj “udomačimo”, si oglejmo preprost poskus s fotoni, ki ga lahko izvedemo tudi doma, saj zanj ne potrebujemo dragega laboratorija. Priskrbeti si moramo le žarnico, ki nam bo služila za izvir fotonov svetlobe, in nekaj polarizacijskih filtrov, ki so danes že povsem običajna oprema vsakega amaterskega fotografa. Polarizacijske filtre lahko izrežemo tudi iz posebnih očal, ki jih dobimo za gledanje tridimenzionalnih filmov. Podobno, kot smo pri elektronu opazovali orientacijo njegovega spina, bomo sedaj pri fotonih preučevali njihovo polarizacijo. Polarizacijo si lahko v prvem približku predstavljamo kot kazalec na fotonu, ki kaže v neko smer, vendar se moramo hkrati zavedati, da ima takšna analogija zelo omejeno veljavnost. Polarizacijski filter deluje na fotone podobno kot rešetka, saj prepušča le tiste, ki so polarizirani v smeri, ki ustreza orientaciji filtra. Filter, katerega orientacija je navpična, bo prepuščal le fotone, katerih lastnost je, da so navpično polarizirani. Ker žarnica oddaja fotone z različnimi polarizacijami, bo filter poskrbel, da bo zaustavil vse fotone, katerih polarizacija ni enaka orientaciji filtra.

Sedaj za prvim filtrom namestimo še drugega in ga usmerimo enako, kot je usmerjen prvi filter. Na prepuščenih fotonih se to ne bo poznalo, saj bodo tisti fotoni, ki so uspeli priti skozi prvi filter, brez težav prišli tudi skozi drugega, ker so polarizirani tako, da jih drugi filter ne bo zadržal. Kaj pa, če drugi filter glede na prvega zasukamo? Skozi oba filtra prihaja vedno manj svetlobe, ko pa sta filtra nameščena pravokotno en na drugega, zadržita vso svetlobo². To je intuitivno povsem sprejemljivo in razumljivo. Če prvi filter prepušča navpično polarizirano svetlobo, drugi filter pa le vodoravno polarizirano, skozi sitem obeh filtrov ne bo prišel noben svetlobni žarek.

Poskusimo dodati še tretji polarizacijski filter. Če ga postavimo za navpično in horizontalno orientirana filtra, ki skupaj ne prepuščata svetlobe, se ne bo nič spremenilo, saj do tretjega filtra ne pride noben foton. Kaj pa če tretji filter namestimo med navpično in horizontalno orientiran filter? Intuitivno pričakujemo, da lahko dodatni filter svetlobo le še dodatno oslabi, ne more pa povzočiti, da bi jo skozi sistem treh filtrov prišlo več kot skozi sistem dveh.

Polarizacijske filtre si lahko predstavljamo tudi kot vrata, skozi katera gredo lahko samo objekti, ki imajo posebej izbrane lastnosti. Navpično polariziran filter si zamislimo kot vrata, skozi katera gredo lahko le moški, ženskam pa je prehod prepovedan. Horizontalno polariziran filter pa si predstavimo z vrati, skozi katere gredo lahko le kadilci, nekadilci pa ne. Če sedaj skozi ta dvoja vrata spustimo gručo ljudi, bodo skozi oboja vrata prišli le moški kadilci. Ženske bodo obtičale že pred prvimi vrati, moški nekadilci pa pred drugimi. Seveda nam intuicija pravi, da lahko pretok z zaporednim dodajanjem novih vrat le zmanjšamo, ne moremo ga pa povečati. Če med oboja vrata namestimo še ena, to nikakor ne more povzročiti, da bi se za drugi vrati pojavila kakšna ženska kadilka ali kaj podobnega. To preprosto ne gre, saj ženske ne smejo že skozi prva vrata.

V kvantnem svetu ta intuitivna logika ne drži več. Če med oba pravokotno polarizirana svetlobna filtra, ki skupaj ne prepuščata svetlobe, namestim še tretji polarizacijski filter, ki ni vzporeden nobenemu od prvotnih dveh filtrov, svetloba spet lahko potuje skozi sistem. Kako to? Po naši analogiji z vrati to pomeni, da se za drugimi vrati, če med oboja vrata dodamo še tretja, pojavijo ženske, kar je nemogoče, saj te niso smele že skozi prva vrata.

Kako si razložimo ta pojav? Svetlobo sestavljajo fotoni, ki so kvantni delci. Pojav lahko pojasnimo le, če privzamemo, da se v stanju fotona, ki je polariziran navpično in je prišel skozi prvi filter, nekako skrivajo tudi nekatera druga polarizacijska stanja. Fotoni, ki pridejo skozi prvi filter, so res v stanju navpične polarizacije, vendar lahko to stanje kvantno opišemo tudi kot superpozicijo dveh drugih stanj, ki skupaj tvorita to stanje. Podobno kot lahko vsak vektor razstavimo na več komponent, katerih vektorska vsota je enaka izhodiščnemu vektorju, lahko tudi stanje fotona, ki opisuje stanje z določeno polarizacijo, razstavimo na dve stanji s polarizacijama usmerjenimi v medsebojno pravokotni smeri. Foton, ki je polariziran navpično, lahko tako opišemo tudi kot foton, ki je v superpoziciji dveh polarizacijskih stanj: stanja polariziranega vzporedno orientaciji drugega filtra in stanja polariziranega pravokotno na orientacijo drugega filtra.

Tako lahko pojasnimo tudi zakaj drugi filter ustavi vse fotone le ko je orientiran pravokotno glede na prvi filter: navpično polarizirano stanje fotona, ki pride skozi prvi filter, ne moremo razstaviti na dve pravokotni komponenti, katerih ena bi bila pravokotna na izvorno stanje. Takšne superpozicije stanj ni, zato noben od navpično polariziranih fotonov ne more skozi drugi horizontalno polarizirani filter.

Problem meritve

Vrnimo se sedaj nazaj k elektronu. Stanje kvantnega sistema formalno opišemo z vektorjem ali žarkom v Hilbertovem prostoru. Za naše potrebe bo dovolj, če si Hilbertov prostor predstavljamo kot nekaj podobnega običajnemu vektorskemu prostoru. Stanje sistema elektrona S, katerega lastnost je, da ima spin gor (mislimo si, da je zelen), bomo to opisali z vektorjem |S+>, sistem v stanju spin dol (mislimo si, da ni-zelen) pa z vektorjem |S->. Ko je sistem v superpoziciji stanj spin gor in spin dol (mislimo si, da je v čudnem stanju, ko ni niti zelen niti ne-zelen oz. oboje), ga opišemo z vektorjem, ki je vsota vektorjev osnovnih stanj spina c₁|S+> + c₂|S->³. V vektorskem prostoru velja pravilo, da je vsota vektorjev ali produkt vektorja s številom tudi vektor. Kot lahko vidimo, je formalni opis superpozicije linearna kombinacija vektorjev stanj, ki predstavljajo med seboj nezdružljive lastnosti sistema. Seveda obstoji veliko različnih kombinacij stanj |S+> in |S->.

Čeprav je nenavadno, da sistem S nima določene vrednosti spina, se lahko še zmeraj nekako izmažemo, saj je elektron premajhen, da bi ga lahko opazovali na način, kot opazujemo npr. košarkarsko žogo. Če je že submikroskopski svet čuden, mogoče vsaj naš običajni makrosvet, v katerem živimo, ni okužen s to prismojenostjo, kot bi rekel Feynman. Morda se kvantnomehanska čudnost izgubi, ko se poskuša prevesti do velikosti celic, žog in galaksij. Lahko bi rekli celo, da se nekako mora skriti, saj v vsakdanjem svetu ne opazimo predmetov, ki bi imeli več nezdružljivih lastnosti hkrati.

Tu pa naletimo na problem. Razvoj kvantnomehanskega sistema v času opisuje Schrödingerjeva enačba. Za nas bo dovolj, če imamo pred očmi dve lastnosti te enačbe: (i) kadarkoli so preizkusili njene napovedi za obnašanje delcev v mikrosvetu, se bile napovedi pravilne in (tu pa nastopi problem) (ii) če veljajo njene napovedi univerzalno, se mora čudnost mikrosveta prenesti tudi na makrosvet. Poskusimo to drugo lastnost pojasniti podrobneje.

Recimo, da imamo merilno napravo (M), ki lahko meri x-spin posameznega elektrona. Ko elektron potuje skozi M, se kazalec na M odkloni navzgor, če ima elektron spin gor, ali navzdol, če ima elektron spin dol. Na začetku poskusa je kazalec na sredini. Opišimo kvantno stanje sistema M, ko kazalec kaže navzgor kot  |M+> in stanje, ko kazalec kaže navzdol z |M->. Sedaj si zamislimo, da pošljemo skozi merilno napravo M elektron S, ki je v superpoziciji stanj spina gor in spina dol. Ker je S v stanju c₁|S+> + c₂|S->, bo po Schrödingerjevi enačbi interakcija med S in M povzročila, da bosta oba po končani meritvi v sestavljenem stanju c₁|S+>|M+> + c₂|S->|M->, kar je superpozicija sestavljenega stanja |S+>|M+> v katerem ima S spin gor in kazalec naprave M kaže navzgor ter sestavljenega stanja|S->|M->, kjer ima S spin dol, kazalec naprave M pa tudi kaže navzdol. V superpoziciji sestavljenih stanj tako nima samo elektron S nedoločene vrednosti spina, ampak tudi kazalec na M ne kaže v nobeno določeno smer, vendar v makrosvetu nikoli ne opazimo kazalcev, ki bi kazali v več strani hkrati.

To nezdružljivost napovedi Schrödingerjeve enačbe in vsakdanjega izkustva je opazil že sam Schrödinger. Opisal jo je v slavnem primeru z mačko. Njegov miselni poskus je potekal takole. Elektron S, merilno napravo M in mačko zaprimo skupaj s stekleničko strupa v škatlo. Kazalec na merilni napravi M povežemo s stekleničko strupa tako, da se bo steklenička razbila in sprostila za mačko smrtonosni strup v primeru, ko se bo kazalec odklonil navzdol. V primeru, ko se bo kazalec odklonil navzgor, pa bo steklenička ostala cela. Vektor |C+> naj predstavlja živo mačko, vektor |C-> pa mrtvo mačko. Po izvedbi meritve bodo po napovedi Schrödingerjeve enačbe sistemi S, M in mačka skupaj v sestavljenem stanju c₁|S+>|M+>|C+> + c₂|S->|M->|C-> v katerem mačka ni ne živa ne mrtva, ampak v superpoziciji živega in mrtvega stanja hkrati⁴. Takšne situacije v naravi seveda ne opazimo, vendar jo Schrödingerjeva enačba napoveduje. Kje je torej meja med kvantnim svetom, ki ga obvladuje Schrödingerjeva enačba in klasičnim svetom, ki ne dopušča superpozicije stanj? Je to 100 atomov, miligram snovi, zavest?

Ortodoksna interpretacija kvantne mehanike

Strogo formalno rečeno, je problem meritve posledica spoja ortodoksne (Dirac – von Neumannove) interpretacije kvantne mehanike in linearnosti kvantne dinamike, ki jo opisuje Schrödingerjeva enačba časovnega razvoja kvantnega stanja. Ortodoksna interpretacija kvantne mehanike je nastala v zgodnjih 1930-ih letih, ko sta  John von Neumann in Paul Dirac uvedla abstraktni matematični formalizem, ki je pod eno streho zajel vse takrat znane formulacije pravil za obnašanje kvantnih delcev – predvsem Schrödingerjevo valovno mehaniko in Heisenbergovo matrično mehaniko. Po Dirac – von Neumannovem abstraktnem formalizmu imamo na eni strani dinamično kvantno stanje, ki ga označuje vektor v Hilbertovem prostoru, na drugi strani pa stanje lastnosti sistema, ki ga predstavljajo merljive fizikalne količine. Če vemo kateri vektor v Hilbertovem prostoru opisuje stanje sistema v nekem trenutku in poznamo sile, ki vplivajo na ta sistem, lahko s pomočjo Schrödingerjeve enačbe napovemo natančen razvoj sistema v prihodnosti. Težava je le, kako povezati dinamično stanje opisano z vektorjem, s stanjem lastnosti sistema, ki jih lahko merimo.

Da bi poudarili razliko med klasično in kvantno mehaniko, v kvantni mehaniki običajno agnostično govorimo o “observablah” namesto o dinamičnih spremenljivkah, ki implicirajo časovni razvoj ves čas določenih vrednosti, kvantno mehaniko pa razumemo kot teorijo, ki podaja le verjetnosti za rezultate meritev observabel. Vsaki observabli (recimo ji R) v Hilbertovem prostoru ustreza množica medsebojno pravokotnih lastnih vektorjev |r_i>, ki v tem prostoru tvorijo ortogonalno bazo. To pomeni, da lahko vektor stanja sistema |s> zapišemo kot linearno kombinacijo baznih vektorjev |r_i>, ki ustrezajo določeni observabli:

|s> = |r_i> + |r_i> + …

Za vsako možno meritev vrednosti r_i observable R, obstoji lastni vektor |r_i>. Merljive vrednosti r_i imenujemo lastne vrednosti observable R, ustrezne vektorje |r_i> pa lastni vektorji ali lastna stanja sistema. Verjetnost, da bomo observabli R izmerili vrednost r_i je enaka |c_i|². V primeru elektrona sta lastni stanji observable x-spina kar |S+> in |S->. Če je sistem elektrona v superpoziciji stanj c₁|S+> + c₂|S->, potem je verjetnost, da bomo izmerili spin gor enaka |c₁|², za spin dol pa |c₂|².

Če vektor, ki opisuje sistem, ni vzporeden kateremu od baznih oz. lastnih vektorjev observable ali – z drugimi besedami rečeno – ni v lastnem stanju observable, observabli ne moremo jasno določiti vrednosti. Lahko ji pripišemo le verjetnost, da bomo pri meritvi izmerili vrednost observable, ki ustreza temu lastnemu stanju. Po ortodoksni interpretaciji imajo observable natančno določeno vrednost le, če je sistem v lastnem stanju te observable. Ta interpretativna vez lastne vrednosti observable in lastnega stanja vektorja ali krajše “e-e vez” (eigenvalue-eigenstate link) je temelj ortodoksne interpretacije kvantne mehanike. Po e-e vezi vektor stanja v vsakem trenutku sinhrono določa verjetnost stanja lastnosti sistema, pod čemer razumemo verjetnost, da bomo za posamezne lastnosti (dinamične spremenljivke) sistema te vrednosti v resnici tudi izmerili, če se v tistem trenutku lotimo meritve. Kvantna mehanika je tako po ortodoksni interpretaciji v svojem bistvu statistična teorija, saj ni stanja kvantnega sistema, v katerem bi imele vse dinamične spremenljivke določene oz. “ostre” vrednosti.

Dinamika kvantnomehanskega stanja je linearna in opisuje jo Schrödingerjeva enačba. Po interakciji dveh kvantnih stanj, kar lahko razumemo tudi kot primer meritve enega sistema nad drugim, stanje skupnega sistema ni lastno stanje merjene observable v interakciji in tudi ne lastno stanje merilne observable, ki jo uporabimo kot kazalec na inštrumentu. Po ortodoksni interpretaciji tako merjena observabla, kot tudi kazalec merilne naprave, nimata ostro določenih vrednosti po interakciji, ki uskladi lego merilnega kazalca z vrednostjo merjene observable. To je formalni opis problema meritve v kvantni mehaniki. Najkrajše bi jo lahko opisali s sklepom: če velja linearna dinamika teorije in interpretativna e-e vez, potem se problemu meritve ne moremo izogniti.

Da bi se izognil problemu meritve, je von Neumann predlagal projekcijski postulat, ki povezuje svet merljivih količin in abstraktni svet vektorjev v Hilbertovem prostoru. Projekcijski postulat pravi, da skoči vektor v Hilbertovem prostoru, ki opisuje stanje sistema, takoj ko izmerimo na sistemu vrednost neke observable, v lego, ki ustreza lastnemu vektorju observable. Vektor stanja sistema se pri meritvi projicira na lastni vektor observable. To seveda pomeni, da ne moremo hkrati izmeriti vrednosti dveh količin sistema (stanja), katerih lastni vektorji v Hilbertovem prostoru niso vzporedni. Von Neumannov postulat temelji na predpostavki, ki se je zdela za realistični opis narave nujna. Če izvedemo na sistemu zaporedoma dve meritvi iste količine, moramo obakrat dobiti enak rezultat, če le ni sistema vmes kaj zmotilo.

Po projekcijskem postulatu meritev na kvantnem sistemu ni več le pasivni odčitek vrednosti določene količine sistema, ampak se ob meritvi spremeni sam sistem. Le tako lahko dasta dve zaporedni meritvi isti rezultat. Proces meritve se tako bistveno razlikuje od drugih procesov v kvantnem svetu. Meritev je po projekcijskem postulatu stohastična projekcija ali kolaps (skok) stanja v eno izmed lastnih stanj merjene količine. Slabost projekcijskega postulata je, da imamo sedaj v igri dva ločena procesa: dinamični razvoj stanja, ki ga opisuje Schrödingerjeva enačba, in še nek drug nelinearen proces, ki ob meritvi projicira stanje na smer lastnega vektorja meritve.

Von Neumannov projekcijski postulat deli svet tako na dva dela: na opazovani sistem in na opazovalca. Schrödingerjeva enačba napoveduje razvoj le za opazovani sistem, dokler ta na pride v stik z opazovalcem. Takrat se vklopi projekcijski postulat in nelinearno spremeni stanje sistema. Von Neumann je celo pokazal, da rezultat napovedi meritve načeloma ni odvisen od tega, na katerem nivoju potegnemo ločnico med opazovanim sistemom in opazovalcem. Pomembno je le, da svet razdelimo na dva dela. To je ortodoksni način razrešitve problema meritve, ki povprečnega laboratorijskega fizika povsem zadovolji. Preden pa si ogledamo še druge modernejše predloge razrešitve problem meritve, si oglejmo še eno nenavadno lastnost kvantnega sveta.

Kvantna prepletenost

Kvantna prepletenost (entanglement) je oznaka za stanje kvantnega sistema v superpoziciji stanj, ki je sestavljen iz dveh ali več podsistemov, kot sta npr. par elektronov ali fotonov. V prepletenem stanju zaradi superpozicije ne moremo prirediti določenega kvantnega stanja vsakemu od posameznih podsistemov. Vektor stanja v Hilbertovem prostoru lahko pripišemo le celotnemu prepletenemu stanju, ne pa posameznim delcev, ki prepleteno stanje sestavljajo.

Oglejmo si primer sistema dveh elektronov. Eno od možnih stanj takega sistema je, da sta oba elektrona vsak v svojem enodelčnem čistem stanju⁵. V takšnem mešanem stanju enodelčnih čistih stanj vsakemu elektronu ustreza svoj vektor stanja in vsak elektron ima svoje lastnosti določene do mere, kot to dovoljuje kvantna mehanika. Nič se ne spremeni, če si sedaj zamislimo statistično mešanico takšnih stanj. Vsak posamezen elektron v mešanici je v določenem stanju in ima svoje lastnosti določene, le mi zanje (še) ne vemo. V tem primeru so rezultati poskusa na takšnem sistemu povsem združljivi z idejo, da so posamezni delci v določenem stanju in tako posedujejo svoje lastnosti.

Z elektroni pa lahko tvorimo tudi kvantne superpozicije stanj in kot bomo videli, so ravno ta prepletena stanja, kjer se elektroni nahajajo v superpoziciji stanj tista, ki imajo nenavadne lastnosti. Najbolj preprost primer prepletenega stanja je primer dveh elektronov (delcev s spinom 1/2), katerih skupni spin je 0. Če v takemu sistemu izmerimo smer spina prvega delca, potem takoj vemo, da je smer spina drugega delca ravno nasprotna. Vendar to ni najbolj pomembna lastnost prepletenega sistema. Za prepleteno stanje je značilno, da ni mogoče določiti kvantnega stanja (tudi nam neznanega ne) vsakemu od posameznih delcev, ki tvorijo prepleteno stanje. Z drugimi besedami povedano: prepleteni posamezni delci nimajo določenega lastnega enodelčnega stanja in tako tudi svojih lastnosti ne, dokler ne izvedemo meritve, ki po ortodoksni interpretaciji “sesuje” zamotano čisto stanje superpozicije v mešano stanje enodelčnih čistih stanj, ki so lastna stanja merjene količine.

Leta 1964 je John Bell pokazal, da lahko s pomočjo prepletenosti napove poskus, s katerim bi lahko napovedal merljivo razliko med napovedmi kvantne mehanike in nekaterih konkurenčnih teorij, ki tudi obravnavajo in interpretirajo dogajanje v mikrosvetu (glej članek: Skrivnostni svet kvantov). Bell je obravnaval sistem para dveh delcev s spinom 1/2, ki sta bila nekoč v interakciji, potem pa se je prostorska razdalja med njima že tako povečala, da med izvedbo poskusa svetlobni signal ne more več prepotovati celotne razdalje od enega do drugega delca. Poskušal je opisati primer para in njegove interakcije z merilno napravo, ki upošteva predpostavke t.i. “lokalno-realističnih” teorij:

• separabilnost – Če sta dva dinamična sistema prostorsko ločena, potem lahko vsakega opišemo le z njegovimi lastnimi lastnostmi, ki niso odvisne od lastnosti drugega sistema daleč stran.
• lokalnost – Noben vpliv prvega sistema ne more neposredno oz. hipno vplivati na drugi sistem, ki je prostorsko ločen od prvega sistema. Meritev na prvem sistemu ne more spremeniti lastnosti drugega sistema, ki je od prvega prostorsko ločen. To načelo v poskusih izpolnijo tako, da se oprejo na posebno teorijo relativnosti, ki pravi, da nič ne more potovati hitreje kot svetloba. Statistična verjetnost napovedi npr. meritve spina prvega delca je lahko odvisna le od lastnosti merilne naprave in lastnosti samega delca, ne pa od meritve spina na drugem delcu, ki je daleč stran.

Bell je uspel pokazati, da bodo dale lokalno-realistične teorije drugačne statistične napovedi za izvedbo poskusa s pari kvantnih delcev v prepletenem stanju kot kvantna teorija. Napovedi kvantne mehanike in lokalno-realističnih teorij so začeli eksperimentalno testirati v 1970-ih, prvi veliki preboj pa je v začetku 1980-ih uspel Alainu Aspectu s sodelavci iz Institut d´Optique iz Pariza. Aspectovi poskusi so potrdili statistične napovedi kvantne mehanike. Izvedeni so bili sicer v razmerah, ki niso bile ravno idealne, a še vedno dovolj dobre, da je uspel poskus večino fizikov prepričati, da narave ni mogoče opisati s pomočjo lokalno-realističnih teorij.

V zadnjih letih je bilo storjenih še nekaj pomembnih eksperimentalnih korakov na tem področju. Skupina Nicolasa Gisina iz ženevske univerze je pred nekaj let potrdila napovedi kvantne mehanike na prepletenih fotonih v medsebojni oddaljenosti več kot 10 km. Ti poskusi so tako kot Aspectovi temeljili na statističnem povprečju veliko ponovljenih meritev. Nasprotno pa so Daniel Greenberger, Michael Horne in Anton Zeilinger (GHZ) leta 1989 pokazali, da je načeloma možno razločiti napovedi kvantne mehanike in lokalno-realističnih teorij tudi znotraj enega samega poskusa, če namesto dveh obravnavamo tri ali več delcev s spinom 1/2. V pristopu GHZ je pod določenimi pogoji možen poskus, za katerega lokalno-realistične teorije z gotovostjo napovedujejo rezultat “da”, kvantna mehanika pa rezultat “ne”. Zeilingerjeva skupina je februarja 2000 v reviji Nature že poročala o prvih uspešnih meritvah, ki potrjujejo napovedi kvantne mehanike⁶.

Predlogi razrešitve problema meritve

Aktualne predloge za razrešitev oz. odpravo problema meritve lahko razvrstimo v tri skupine:

1. V prvi skupini so predlogi, ki sprejmejo ortodoksno interpretacijo, a spremenijo linearno dinamiko teorije. Trenutno je v igri več predlogov spremembe dinamike, med katerimi ima morda največ možnosti za uspeh predlog Ghirardija, Riminija in Webera, ki mu pravijo tudi GRW teorija. V prvo skupino bi lahko uvrstili tudi Penrosove predloge kvantne gravitacije…
2. Druga možnost je sprejetje linearne dinamike in zavrnitev ortodoksne interpretacije. To so t.i. predlogi interpretacij kvantne mehanike “brez sesutja” (no collapse), ki zavračajo predvsem von Neumannov projekcijski postulat. Sem spadajo npr. Bohmove zgodnje teorije s skritimi spremenljivkami, Everettova interpretacija relativnega stanja popularno imenovana tudi interpretacija “več svetov”, pa tudi modalna interpretacija…
3. Tretja skupina zajema predloge, ki sprejemajo tako ortodoksno interpretacijo, kot tudi linearno dinamiko teorije, hkrati pa poskušajo pokazati, da lahko razliko med mešanico stanj, ki jih po meritvi zahteva ortodoksna interpretacija, in čistim stanjem, ki ga predvidi linearna dinamika, zanemarimo za vse praktične namene (for all practical purposes – FAPP). Sem uvrščamo teorije, ki trdijo, da vektor stanja sploh ne opisuje posameznega kvantnega delca, ampak le skupino (ensemble) enako pripravljenih delcev, kot tudi teorije dekoherence (Zurek, Gell-Mann, Omnès…), ki trdijo, da stanje merilne naprave v superpozicij (koherenci) zaradi vpliva okolice na merilno napravo zelo hitro preneha biti v superpoziciji (dekoherira). Vsako makroskopsko telo je namreč v neprestanem stiku s svojo okolico, zato postane njegovo kvantno stanje z okolico zelo hitro prepleteno. Opis mačke v superpoziciji živega in mrtvega stanja bi morali tako preplesti še s stanjem stekleničke strupa, merilne naprave, škatle… Za takšno prepleteno stanje pa kvantna mehanika predvideva, da je vsaka meritev zgolj na njegovem delu (recimo na mački) brez hkratne meritve tudi na okolici, praktično neločljiva od meritve na mešanici stanj, ki ni v superpoziciji, zaradi česar superpozicije stanj v makrosvetu praktično nikoli ne moremo opaziti. Pred kratkim sta Serge Haroche in Jean-Michel Raimond s sodelavci na Ecole Normale Supérieure v Parizu izvedla poskus, v katerem sta pojav dekoherence neposredno opazovala na skupini fotonov.

Danes ima izmed vseh predlogov za razrešitev problema meritve največ pristašev prav predlog dekoherence – nekateri mu pravijo kar “nova ortodoksnost” -, saj ne zahteva spreminjanja med fiziki ustaljene “šolske” interpretacije teorije, ki jo lahko najdemo v večini učbenikov kvantne mehanike. Vendar kar nekaj uglednih teoretikov v “odrešujočo” moč dekoherence ne verjame povsem, ker so prepričani, da dekoherenca temeljnega problema kvantne meritve pravzaprav sploh ne razreši, ampak le pospravi pod preprogo.

*

V začetku 20. stoletja so nove fizikalne teorije temeljito spremenile klasični pogled na naravo. S posebno teorijo relativnosti je geometrija izgubila mesto apriorne vede in smiselno je postalo spraševanje po “pravi” geometriji sveta. S splošno teorijo relativnosti je geometrija postala ne le empirična, ampak tudi dinamična, saj se lahko spreminja v odvisnosti od porazdelitve mase in energije. Na enak način kot je relativnost spremenila razumevanje geometrije, je kvantna mehanika na novo postavila obravnavo razmerja med možnim in dejanskim v svetu. V klasični fiziki (tu imamo v mislih vse teorije, ki niso kvantne) spremembe stanja sistema opišemo z zakoni, ki obravnavajo in napovedujejo časovni razvoj dejanskih lastnosti sistema. V kvantni fiziki pa teorija ne napoveduje neposredno dinamike dejanskih lastnosti sistema, ampak se dinamično spreminjajo možne lastnosti sistema, ki jih opisuje vektor stanja v Hilbertovem prostoru. V kvantnem svetu je torej na delu dvojna dinamika: Schrödingerjeva dinamika, ki opisuje razvoj možnega, dinamika tega, kar se dejansko spreminja skozi čas, pa mora slediti in se prilagajati razvoju strukture možnosti.

Literatura

• D.Z. Albert. 1993. Quantum Mechanics and Experience. Cambridge, Mass: Harvard University Press.
• J. Bub. 1997. Interpreting the Quantum World. Cambridge: Cambridge University Press.
• R.I.G. Hughes. 1989. The Structure and Interpretation of Quantum Mechanics. Cambridge, Mass: Harvard University Press.
• R. Omnès. 1999. Understanding Quantum Mechanics. Princeton: Princeton University Press.
• J.A. Wheeler, W.H. Zurek. 1983. Quantum Theory and Measurement. Princeton: Princeton University Press.
• Članki o kvantni mehaniki v The Stanford Encyclopedia of Philosophy.

Sašo Dolenc, kvarkadabra.net – številka 5 (junij 2000)

-