Einsteinove posebne teorije relativnosti se že skoraj sto let je drži avra zapletenosti in nerazumljivosti. Z branjem sestavka se lahko prepričaš, da osnov teorije relativnosti – v nasprotju s popularnim mitom – sploh ni težko razumeti. Teorija zahteva le, da o vsakdanjih stvareh razmišljaš na malo drugačen, nov način. Poskusi!
Einsteinova revolucija v razumevanju prostora in časa
“Zdravi razum ni nič drugega kot skupek predsodkov, ki se naberejo v možganih pred osemnajstim letom starosti.” (Albert Einstein)
Zamisli si, da si z zelo dolgim metrom izmeril(a) razdaljo, ki jo vsak dan prehodiš med domom in službo (ali šolo). Nameril si natanko 5 km. Svoji meritvi povsem zaupaš, zato si takoj pripravljen s prijateljem staviti, da bo tudi števec kilometrov v njegovem avtomobilu, za isto pot pokazal točno 5 km, če le ni pokvarjen. Podobno bi stavil tudi glede časa, ki ga porabiš za pot v službo. Recimo, da se tvoj prijatelj vozi po mestu z avtom, ko ga zjutraj ob 7:00 pokličeš po mobilnem telefonu v trenutku, ko zapuščaš domačo hišo, in spet ob 7:45, ko prispeš v službo. Seveda bi te zelo presenetilo, če bi prijateljeva ura med obema klicema izmerila časovni interval, ki ne bi bil dolg točno 45 minut.
Razdalje in časi se zdijo v vsakdanjem življenju absolutni. Intuitivno namreč pričakujemo, da se bomo glede razdalje med dvema točkama (npr. med domom in službo) vsi strinjali. Podobno pričakujemo, da med nami ne bo razhajanj glede izmerjene dolžine časa med dvema dogodkoma (npr. odhod od doma in prihod v službo). Prav zato so bili vsi zelo presenečeni, ko je Albert Einstein leta 1905 s teorijo relativnosti pokazal, da naša intuitivna pričakovanja niso povsem pravilna. Z zelo natančnim merjenjem bi namreč lahko ugotovil, da tvoja meritev razdalje med domom in službo ni enaka razdalji, ki jo je izmeril prijatelj v avtomobilu. Prav tako se s prijateljem ne bi strinjala glede izmerjenega časa, ki si ga porabil za pot od doma do službe. Pri običajnih hitrostih bi bila razlika obeh meritev neznatna, vendar bi postala veliko bolj opazna v primeru, če bi prijatelj po cesti drvel s hitrostjo blizu svetlobne hitrosti.
Razhajanja opazovalcev glede meritev razdalj in časov so le del osupljivih idej, ki jih vsebuje teorija relativnosti. Einstein jo je razvil v dveh delih: posebna teorija relativnosti, ki jo je objavil leta 1905, je pokazala, da se prostor in čas prepletata, a se ni ukvarjala z učinki gravitacije; splošna teorija relativnosti, ki jo je predstavil leta 1915, pa je podala presenetljivo nov pogled na gravitacijo – pogled, ki je omogočil obravnavo razširjanja in usode vesolja kot celote in nenavadnih objektov v njem kot so npr. črne luknje (glej tekst Prostor-čas in gravitacija: uvod v splošno teorijo relativnosti).
V sestavku se bomo posvetili predvsem novemu pogledu na prostor in čas v posebni teoriji relativnosti. Ogledali si bomo, kako teorija utemelji naslednje ideje:
- Nič ne more potovati hitreje, kot potuje svetloba po praznem prostoru; noben predmet iz snovi ne more svetlobne hitrosti nikoli niti doseči, kaj šele preseči.
- Če pazljivo opazuješ predmet ali osebo, ki se giblje mimo s hitrostjo blizu svetlobne hitrosti, bo za gibajočo se stvar čas tekel počasneje. Torej se gibajoča oseba stara počasneje od tebe, gibajoča se ura tiktaka počasneje kot tvoja zapestna ura, gibajoči se računalnik dela počasneje kot enak računalnik na katerega tipkaš, ipd.
- Če opaziš, da sta se dva dogodka, kot sta npr. svetlobna bliska na različnih krajih ob istem času, dogodila hkrati, se oseba, ki se giblje zate s hitrostjo blizu svetlobne hitrosti, glede te ugotovitve ne bo strinjala; zanjo dogodka nista sočasna.
- Če pazljivo izmeriš dolžino predmeta, ki se zate giblje s hitrostjo blizu svetlobne hitrosti, boš opazili, da je njegova dolžina v smeri gibanja krajša od dolžine, ki bi jo izmerili, če se objekt ne bi gibal.
- Če bi lahko izmeril maso predmeta, ki se zate giblje s hitrostjo blizu svetlobne hitrosti, bi ugotovil, da je masa gibajočega se predmeta večja, kot bi jo izmeril, če bi predmet stal na mestu. Iz te ugotovitve lahko sklepaš – kot je to storil tudi Einstein – da velja enačba E=mc2.
Čeprav se ti morda zdijo naštete posledice teorije relativnosti čudaške, so danes podprte že z zelo velikim številom opazovanj in poskusov. Prav tako vse naštete ugotovitve logično sledijo iz nekaj preprostih idej. Če te ne bo preveč obremenjevala intuicija vsakdanjega sveta, in če boš globoko razmislil o vsebini, ki jo boš prebral, boš kmalu spoznal vso skrivnost relativnosti in postal vešč v njenih idejah.
Kaj je relativnost?
Zamisli si letalo, ki z nadzvočno hitrostjo 1650 km/h leti iz Nairobija v Keniji proti Quitu v Ekvadorju. Kako hitro pravzaprav leti to letalo? Na prvi pogled je vprašanje trivialno, saj smo ravnokar rekli, da potuje s hitrostjo 1650 km/h. Ampak … Nairobi in Quito oba ležita skoraj na Zemljinem ekvatorju in ekvatorialna hitrost Zemljinega vrtenja je prav tako 1650 km/h. Med poletom od vzhoda na zahod, iz Nairobija v Quito, potuje letalo v nasprotni smeri vrtenja Zemlje. Če bi opazovali letalo iz vesolja, bi izgledalo, kot da miruje nad oblaki, medtem ko se Zemlja pod njim vrti. Ko bi se polet začel, bi videli letalo, kako bi vzletelo iz letališča v Nairobiju, potem bi nepremično lebdelo v zraku, spodaj pa bi Zemljina rotacija odnašala Nairobi vedno bolj stran in Quito vedno bliže letalu. Ko bi se Quito končno povsem približal, bi se letalo samo še spustilo z višine in pristalo na letališču.
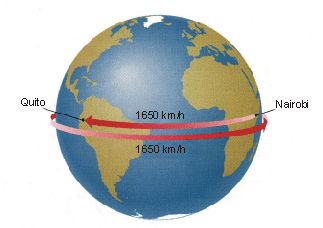
Sedaj imamo dve alternativni interpretaciji leta letala: ljudje na Zemlji bodo rekli, da je letalo letelo proti zahodu nad Zemljino površino, opazovalci v vesolju pa bodo trdili, da je letalo ves čas mirovalo, v smeri vzhoda pa se je vrtela le Zemlja pod njim. Obe interpretaciji sta seveda enako pravilni. Pravzaprav je še veliko enako pravilnih pogledov na let letala. Opazovalec, ki bi opazoval celotni Sončev sistem, bi videl, da se letalo giblje s hitrostjo več kot 100.000 km/h, kar je hitrost kroženja Zemlje okoli Sonca. Opazovalec, ki živi v oddaljeni galaksiji, bi videl letalo, ki se skupaj z Zemljo in Rimsko cesto zaradi razširjanja vesolja oddaljuje z zelo veliko hitrostjo. Vsi opazovalci pa bi se strinjali vsaj o eni stvari: letalo se giblje s hitrostjo 1.650 km/h glede na površino Zemlje.
Na primeru letala smo ugotovili, da vprašanja kot so: “Kdo se zares giblje?” in “Kako hitro se giblješ?” nimajo absolutnih odgovorov. Einsteinova teorija relativnosti je dobila ime po predpostavki, da je merjenje gibanja, kot tudi merjenje časa in prostora, smiselno le, če povemo, relativno glede na kaj oz. koga smo nekaj izmerili. Vendar pozor! Teorija relativnosti ne trdi, da je vse relativno. Vsaj dve stvari v vesolju sta po teoriji relativnosti absolutni:
- zakoni narave so za vse opazovalce enaki in
- vsi opazovalci vedno izmerijo isto vrednost za svetlobno hitrost.
Kot bomo kmalu videli, lahko iz zgornjih dveh nedolžnih stavkov izpeljemo vse presenetljive posledice relativnosti, ki smo jih prej našteli.
Kako misliti relativno?
Razlog, zakaj ima relativnost sloves težko razumljive teorije kljub temu, da je v svojem bistvu zelo preprosta, je v tem, da se z večino njenih idej in posledic ne srečamo v vsakdanjem življenju. Vplivi relativnosti se pokažejo šele, ko imamo opravka s hitrostmi, ki so blizu svetlobne hitrosti ali pa z gravitacijskimi polji, ki so veliko večja kot so na Zemlji. Ker ponavadi nimamo izkušenj s takšnimi skrajnimi razmerami, nimamo nobenega intuitivnega občutka zanje. Trditve, da teorija relativnosti krši zdravi razum, zato niso povsem točne. Teorija relativnosti se povsem sklada z vsem, kar se nam dogaja v vsakdanjem življenju.
Relativnost boš razumel le, če se naučiš gledati vsakdanje izkušnje v novi, širši perspektivi. Na srečo si se moral nekaj podobnega nekoč že naučiti. V rani mladosti si se npr. navzel običajnega pomena besed spodaj in zgoraj: zgoraj je nad glavo, spodaj pa proti nogam; stvari po svoji naravi padajo navzdol. Nekega dne pa so te poučili, da je Zemlja okrogla. Ko si pogledal globus s severno poloblo obrnjeno navzgor, si bil takoj soočen s paradoksom – s situacijo, ki je nasprotovala zdravemu razumu oz. bila v protislovju sama s sabo. Tvoj zdravi razum je trdil, da bi morali Avstralci pasti z Zemlje, hkrati pa si vedel, da to ni res. Da bi paradoks razrešili, si se moral sprijazniti, da tvoje zdravorazumsko razumevanje pojmov zgoraj in spodaj ni povsem pravilno. Prisiljen si bil sprejeti novo razumevanje obeh pojmov, kjer navzdol pomeni proti središču Zemlje, navzgor pa nasprotno smer.
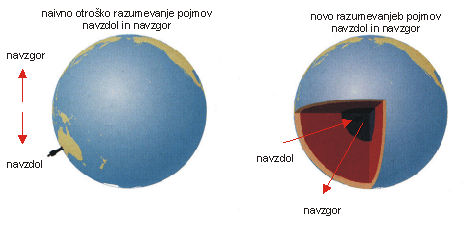
Kot najstnik se je Einstein spraševal, kako bi izgledal svet, če bi potoval skozenj s svetlobno hitrostjo ali še hitreje? Ko je razmišljal o vprašanju, je vedno naletel na protislovja. Paradokse je dokončno razrešil šele, ko je ugotovil, da moramo svoje zdravorazumsko razumevanje prostora in časa spremeniti, če ju želimo razširiti tudi na področje visokih hitrosti in močnih gravitacijskih polj. Kot smo se nekoč naučili drugačnega razumevanja pojmov navzdol in navzgor, se moramo sedaj spopasti z novim razumevanjem prostora in časa.
Relativno gibanje in miselni poskusi
“Če bi se res motil, bi bil en profesor povsem dovolj.” (Albert Einstein o knjigi, v kateri ga je 100 nacističnih profesorjev obtoževalo, da je njegova teorija relativnosti napačna.)
Relativnost bomo preučevali s pomočjo miselnih poskusov, v katerih bomo ustvarili namišljene situacije in jim poskušali miselno slediti. Oporna točka naših miselnih poskusov bo privzetek, da sta obe temeljni načeli relativnosti (t.i. absoluta relativnosti) resnični.
Prvo obeh načel, da so zakoni narave za vse enaki, verjetno ni presenetljivo. Če si na letalu z zagrnjenimi okni med zelo mirnim letom, gibanja sploh ne boš čutil. Pričakuješ lahko, da boš prišel do enakih rezultatov pri kateremkoli poskusu, ki ga boš izvedel na letalu, do kakršnih bi prišel tudi nekdo drug, ki bi poskus izvajal na trdnih tleh. Enaki rezultati dokazujejo, da veljajo isti zakoni narave v letalu in na trdnih tleh. V jeziku relativnosti predstavljata letalo in trdna tla dva različna opazovalna sistema (frame of reference), ki se gibata relativno drug na drugega. Ideja, da so zakoni narave za vse enaki, pomeni, da niso odvisni od konkretnega opazovalnega sistema.
Drugo načelo relativnosti, da je hitrost svetlobe za vse enaka, je mnogo bolj nenavadno.V splošnem pričakujemo, da izmerijo ljudje v različnih opazovalnih sistemih različne hitrosti za isti gibajoči se predmet. Kot primer si zamisli kroglico, ki jo zakotališ po sredini letala. Kroglica se bo v opazovalnem sistemu letala gibala počasi, v sistemu opazovalca na tleh, pa bo imela še dodatno hitrost samega letala, po katerem se kotali. Vendar pa bo v primeru, ko v letalu posvetiš z baterijsko svetilko in izmeriš hitrost izsevane svetlobe, opazovalec na tleh izmeril povsem enako svetlobno hitrost. Opazovalci v različnih opazovalnih sistemih se ne strinjajo glede izmerjenih hitrosti snovnih teles, a vsi zmeraj izmerijo enako vrednost za hitrost svetlobe, ne glede na to, od kje svetloba prihaja.

Kako vemo, da vsakdo zmeraj izmeri enako hitrost svetlobe? Einstein je prišel do takšnega sklepa, ker je le tako lahko razrešil protislovja, na katere je naletel, ko je razmišljal, kako bi izgledal svet, če bi skozenj potoval s svetlobno hitrostjo. Vendar so lahko le opazovanja in poskusi pravi razsodnik za sodbe o znanstvenih teorijah. Mnogo opazovanj in poskusov je potrdilo, da je svetlobna hitrost resnično absolutna količina v naravi. Absolutnost svetlobne hitrosti je eksperimentalno potrjeno dejstvo.
Mogoče ta trditev na prvi pogled ne izgleda pomembno, vendar te bo prisilila, da opustiš marsikatero od ustaljenih intuitivnih prepričanj o zgradbi in delovanju sveta. Zakaj je ta trditev tako prelomna, bomo raziskali s pomočjo nekaj miselnih poskusov o relativnem gibanju, kot ga vidijo opazovalci v različnih opazovalnih sistemih. Ker posebna teorija relativnosti ne obravnava učinkov gravitacije, si miselne poskuse najlaže predstavljamo, če si zamislimo, da se dogajajo nekje globoko v vesolju, daleč stran od vseh gravitacijskih polj. Uporabili bomo vesoljske ladje, ki prosto lebdijo z ugasnjenimi motorji. Ker je vse v in okoli teh vesoljskih ladij v breztežnosti in prosto lebdi, bomo imenovali opazovalne sisteme v teh vesoljskih ladjah prostolebdeči (njihovo uradno ime je inercialni opazovalni sistemi).
Miselni poskusi pri običajnih hitrostih
Da preverimo, kako domač si z idejami o relativnem gibanju, ki ga srečujemo v vsakdanjem življenju, najprej analizirajmo nekaj miselnih poskusov z običajnimi predmeti pri običajnih hitrostih.
Miselni poskus 1: Predstavljaj si, da prosto lebdiš v vesoljski ladji. Ker gibanja ne občutiš, se ti zdi, da miruješ oz. da potuješ s hitrostjo nič. Ko pogledaš skozi okno, opaziš prijateljico Tino v svoji vesoljski ladji, ki se od tebe oddaljuje s hitrostjo 90 km/h. In kako vidi dogajanje Tina? Na vprašanje lahko odgovorimo, če situacijo poskusa logično analiziramo. Ker se Tina zate giblje s konstantno hitrostjo, mora biti tudi ona v prostolebdečem opazovalnem sistemu. Za samo sebe tako čuti, da miruje, zate pa je prepričana, da se od nje oddaljuješ s hitrostjo 90 km/h. Posebej poudarimo, da imata prav oba s Tino. Oba bi prišla do enakih rezultatov pri vseh poskusih, ki bi jih izvedla, in našla enake zakone narave. Lahko bi se v neskončnost prerekala, kdo se pravzaprav giblje, a bi bila polemika povsem neproduktivna, ker je vse gibanje relativno.
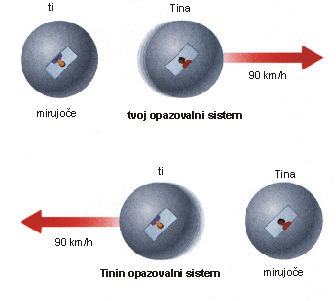
Miselni poskus 2: Začnimo z enako situacijo kot v miselnem poskusu 1, le da sedaj oblečeš skafander in stopiš ven iz svoje vesoljske ladje. V roki držiš malo žogo, ki jo zalučaš proti Tini s hitrostjo 100 km/h. Kako hitro se giblje žoga glede na Tino? S tvojega stališča se Tina in žoga gibljeta v isto smer. Tina s hitrostjo 90 km/h, žoga pa s hitrostjo 100 km/h. Žoga je za 10 km/h hitrejša od Tine, zato jo bo prej ali slej dohitela in odletela mimo njene ladje. S stališča Tine, pa se ti giblješ stran s hitrostjo 90 km/h. Tina torej vidi, da se ji žoga približuje s hitrostjo 10 km/h – hitrost žoge glede nate je 100 km/h minus 90 km/h s katerimi se giblješ relativno glede na Tino. Pomembno je, da se s Tino strinjata, da bo žoga letela mimo Tine z relativno hitrostjo 10 km/h.
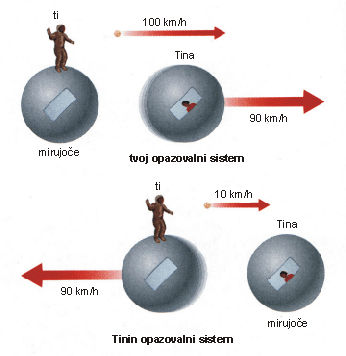
Miselni poskus 3: Tokrat vržeš žogo proti Tini s hitrostjo 90 km/h. Zdi se ti, da potuje žoga s povsem enako hitrostjo kot Tina, zato boš žogo ves čas videl lebdeti ob Tinini vesoljski ladji. S Tininega stališča se 90 km/h, s katerimi si zalučal žogo natančno ujema s 90 km/h, s katerimi se oddaljuješ od njene ladje, zato Tina vidi, da žoga zanjo miruje. Razmisli za trenutek o naslednjem: preden si žogo vrgel, jo je videla Tina, kako se s tabo vred oddaljuje s hitrostjo 90 km/h. V trenutku, ko jo vržeš, pa žoga nenadoma v Tininem opazovalnem sistemu miruje, ostaja na mestu v stalni oddaljenosti od njene vesoljske ladje. Tudi mnogo ur kasneje, ko boš že daleč, bo Tina še zmeraj videla žogo lebdeti na istem mestu. Če želi, si lahko obleče skafander in jo gre ven iskat, ali pa jo pusti tam kjer je, saj se ne bo premaknila nikamor.
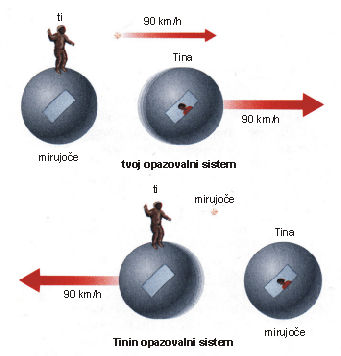
Miselni poskusi pri velikih hitrostih
Absolutnost svetlobne hitrosti v prvih treh miselnih poskusih ni igrala pomembne vloge, ker so bile relativne hitrosti teles zelo majhne v primerjavi s hitrostjo svetlobe. 100 km/h je npr. le 1 deset milijoninka svetlobne hitrosti. Poskusimo sedaj hitrosti povečati in raziskati nenavadne posledice, ki jih prinese absolutnost svetlobne hitrosti.
Miselni poskus 4: Zamisli si, da se Tina oddaljuje z 90 % svetlobne hitrosti ali 0,9c. (c je simbol za svetlobno hitrost, ki znaša približno 300 000 km/s). Kako vidi dogajanje Tina? Z razliko, da so hitrosti večje, je vse enako, kot pri poskusu številka 1. Tini se zdi, da miruje, tebe pa vidi, da se oddaljuješ s hitrostjo 0,9c.
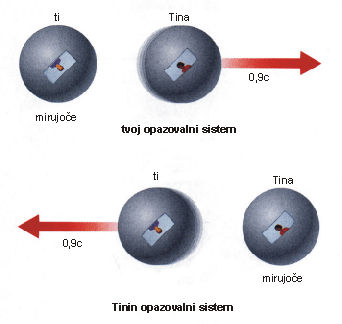
Miselni poskus 5: Sedaj pa namesto, da bi metal žogo, splezaš iz vesoljske ladje in posvetiš s svetilko v smeri Tinine ladje. Kako se giblje svetlobni žarek glede na Tino? Vidiš, da se gibljeta Tina in svetlobni žarek oba v isto smer. Tina potuje z 90% svetlobne hitrosti ali 0,9c, svetlobni žarek pa s polno svetlobno hitrostjo ali c. Svetlobni žarek se zate giblje tako za 0,1c hitreje od Tine. Do sedaj nas ugotovitve poskusa še niso presenetile. Tini se zdi, da ona miruje in da se ti oddaljuješ s hitrostjo 0,9c. V skladu z zdravorazumsko logiko, ki smo ga uporabljali v prejšnjih poskusih, bi sedaj lahko rekli, da se svetlobni žarek Tini približuje s hitrostjo 0,1c = svetlobna hitrost minus tvoja hitrost 0,9c. Vendar je ta odgovor napačen! Relativnost pravi, da je svetlobna hitrost vedno in za vse enaka. Tina mora tako videti, da se ji svetlobni žarek približuje s hitrostjo c in ne 0,1c.
S Tino se tako ne strinjata več o relativni hitrosti svetlobnega žarka glede na Tinino raketo. Tina bo videla, da je svetlobni žarek potoval mimo nje s hitrostjo svetlobe c, medtem ko bo zate potoval le za 0,1c hitreje od Tinine ladje. Po starem zdravorazumskem sklepanju zveni naša ugotovitev absurdno. Vendar smo do nje prišli s preprosto logiko iz predpostavke, da je svetlobna hitrost enaka za vse opazovalce. Dokler je ta predpostavka točna – in absolutnost svetlobne hitrosti je eksperimentalno potrjeno dejstvo – so naši zaključki povsem smiselni.
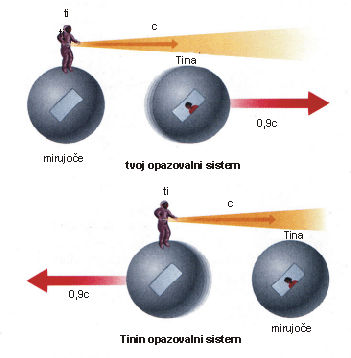
Svetlobne hitrosti ne moreš doseči
Morda se sprašuješ, kaj bi Tina videla, če bi se oddaljevala s svetlobno hitrostjo ali mogoče še hitreje? Tudi sam Einstein si je zastavil natanko enako vprašanje, ko se je prvič spopadel s skrivnostnim svetom velikih hitrosti. Vendar, ko enkrat priznamo absolutnost hitrosti svetlobe za dejstvo, ni težko pokazati, da noben snovni predmet nikoli ne more doseči svetlobne hitrosti oz. še manj jo preseči.
Miselni poskus 6: Pravkar si zgradil najboljšo raketo kar si jih lahko zamisliš in popelješ jo na testni let. Kmalu potuješ hitreje, kot je uspel potovati kdorkoli prej. Nato prestaviš v še višjo prestavo. Giblješ se vse hitreje in hitreje. Sedaj se soočiš s ključnim vprašanjem: lahko pospešiš do hitrosti, ki je večja od hitrosti svetlobe? Preden odgovorimo na to vprašanje, nas dejstvo, da so vsa gibanja le relativna, sili, da si postavimo podvprašanje: v katerem opazovalnem sistemu pravzaprav meriš hitrost svoje ladje? Začnimo z tvojim lastnim opazovalnim sistemom. Zamisli si, da prižgeš na raketi prednje žaromete. Ker je hitrost svetlobe absolutna, moraš videti, da se svetloba pred tabo oddaljuje s hitrostjo 300 000 km/s. To je dejstvo, ki mora držati ne glede na to, za koliko si vesoljsko ladjo že pospešil. V svojem lastnem opazovalnem sistemu nikoli ne boš mogel dohiteti ali prehiteti svetlobe s tvojih lastnih prednjih žarometov.
Ali lahko kdo v drugem opazovalnem sistemu reče, da se zanj giblješ hitreje kot svetloba? Opazovalci v različnih opazovalnih sistemih bodo tvojo hitrost izmerili različno, a vsi opazovalci se bodo med seboj strinjali o dveh ključnih zadevah: (1) svetloba s tvojih žarometov te prehiteva in (2) svetloba se giblje s hitrostjo 300 000 km/s. Torej, če te prehiti svetloba in, če svetloba potuje s svetlobno hitrostjo, moraš torej potovati počasneje od svetlobe (svetlobne hitrosti). Ni pomembno kdo meri tvojo hitrost; lahko si to ti, lahko je nekdo na Zemlji, ali kdorkoli drug v kateremkoli opazovalnem sistemu. Nihče te ne more videti potovati s hitrostjo svetlobe.
Če te to še zmeraj ni prepričalo, okoliščine preprosto obrnimo. Predstavljaj si, da bežiš z negostoljubnega planeta. Nekdo na planetu posveti za teboj s svetlobnim žarkom. Ker je hitrost svetlobe absolutna, te bo žarek prehitel s hitrostjo 300.000 km/s. Za osebo na planetu pa se bo žarek gibal z enako hitrostjo 300.000 km/s, hkrati pa bo lahko videla, kako je žarek hitrejši kot ti. Tako se bodo ponovno vsi opazovalci strinjali, da se giblješ počasneje kot svetloba. Enak argument lahko uporabimo za vsak gibajoči se predmet. Dokler je svetlobna hitrost absolutna, noben predmet snovi ne more dohiteti ali prehiteti svetlobe. Da bi zgradili vesoljsko ladjo, ki bi potovala s svetlobno hitrostjo, tako ni le tehnološko težko izvedljivo, ampak preprosto sploh ni izvedljivo.
Relativnost prostora in časa
“Gospod je vzvišen, ni pa zloben.” (Albert Einstein)
V začetku smo našteli nekaj pomembnejših napovedi teorije relativnosti. Do sedaj smo pokazali le, kako prva (noben materialni objekt ne more potovati s hitrostjo svetlobe ali hitreje) sledi iz obeh absolutov relativnosti. V nadaljevanju si oglejmo, zakaj moramo nujno spremeniti tudi razumevanje starih pojmov prostora in časa.
Čas teče različno v različnih opazovalnih sistemih
V pripravah na naš naslednji miselni poskus si zamisli, da si na gibajočem se vlaku in mečeš žogico v zrak tako, da se odbije od stropa in ti ponovno pade v dlan. Kako bi izgledali pot in hitrost žogice za opazovalca, ki miruje na železniški postaji, medtem ko se ti pelješ mimo njega na vlaku? Kot si lahko ogledamo na sliki, vidi opazovalec s postaje žogico, kako se giblje skupaj z vlakom in pri tem poskakuje do stropa, tako da se pri vsakem skoku navidezno premakne naprej po progi. Ker opazovalec s postaje opazi, da se žogica, poleg tega, da poskakuje do stropa, premika še s hitrostjo vlaka, bo zanjo izmeril večjo hitrost, kot jo izmeri opazovalec na vlaku. Če se vlak giblje počasi, bo razlika izmerjenih hitrosti obeh opazovalcev minimalna. V primeru velike hitrosti vlaka, pa je razlika obeh hitrosti občutna.

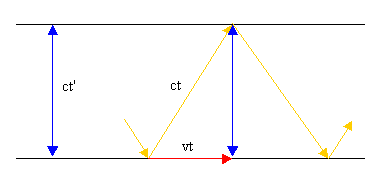
Miselni poskus 7: V svoji vesoljski ladji pritrdi Tina na tla laser in ga usmeri na zrcalo, ki je pritrjeno na strop. Nato z laserjem za trenutek posveti in z zelo natančno uro izmeri čas, ki ga žarek porabi, da prepotuje pot od tal do stropa in nazaj. Ko Tinina vesoljska ladja potuje mimo, skozi okno opazuješ njen poskus. S svojo zelo natančno uro izmeriš čas, ki ga žarek potrebuje od Tininih tal do stropa in nazaj. Ker se Tina, laser in ogledalo glede na tvojo ladjo premikajo, vidiš svetlobni žarek rahlo poševno, ko potuje od tal do stropa in nazaj. V tvojem opazovalnem sistemu se torej zdi, da potuje svetloba po daljši poti kot to vidi Tina, podobno kot je opazovalec na postaji videl, da se žogica giblje po daljši poti kot opazovalec na vlaku.
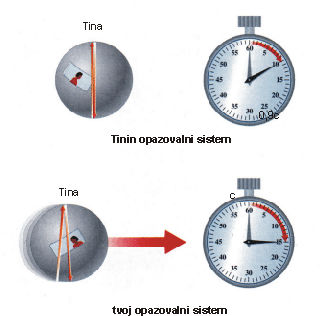
Za običajni zdravorazumski pogled to ne bi bilo nič nenavadnega. S Tino bi se strinjala, koliko časa porabi žarek za pot od tal do stropa in nazaj, podobno kot je bilo to pri žogici na vlaku. Daljšo pot bi lahko razložil tako, da bi rekel, da se je svetloba zate gibala hitreje kot za Tino. Vendar pa, ker imamo opravka s svetlobo, morata oba s Tino izmeriti za svetlobo vedno enako hitrost 300.000 km/s, tudi če je njena pot nagnjena. Kaj torej storiti? Za oba s Tino je svetlobna hitrost enaka, vendar vidiš ti žarek prepotovati po daljši poti, zanjo pa, če se strinjamo, da je hitrost enaka, žarek porabi več časa. Tvoja ura bo tako izmerila za eno pot žarka po Tinini raketi od tal do stropa in nazaj daljši čas, kot ga bo izmerila Tina. Če skozi okno opazuješ Tinino uro, boš tako videl, da teče počasneje kot tvoja lastna. Pri tem ni pomembno, kako s Tino merita čas. Vsaka ura bo tekla počasneje v Tininem opazovalnem sistemu, če jo opazuješ iz tvoje ladje. Mehanične, elektronske, kvarčne ali atomske ure, bitje srca, hitrost biokemičnih reakcij, vse bo teklo počasneje. Miselni poskus lahko torej zaključimo z osupljivo ugotovitvijo, da teče čas za Tino počasneje kot v tvojem opazovalnem sistemu.
Za koliko teče Tinin čas bolj počasi, je odvisno od njene relativne hitrosti glede nate. Če je njena hitrost majhna v primerjavi s svetlobno hitrostjo, razlike skorajda ne boš opazil. Večja ko pa je njena hitrost, bolj je pot žarka nagnjena in večja je razlika v hitrosti teka obeh ur. Če posplošimo, pridemo do naslednjega zaključka: gledano iz tvojega opazovalnega sistema, teče čas za kogarkoli, ki se glede nate giblje, počasneje. Hitreje, ko se drugi opazovalni sistem giblje, počasneje teče čas v njem. Ta pojav imenujemo dilatacija časa, ker nam pove, da se čas raztegne v gibajočem se opazovalnem sistemu.
| Izpeljava enačbe za dilatacijo časa
Poskusimo izpeljati še enačbo zakasnitve Tininega časa glede na tvojega. Pomagali si bomo z lasersko uro, ki smo jo spoznali v miselnem poskusu 7. Sklepajmo:
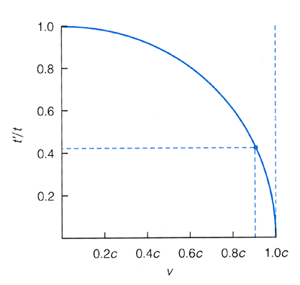
Dobili smo enačbo dilatacije časa, ki nam poda razmerje med hitrostjo teka časa v gibajočem se (t’) in mirujočem (t) opazovalnem sistemu v odvisnosti od relativne hitrosti (v) enega sistema glede na drugega. Iz grafa enačbe odvisnosti razmerja t’/t od relativne hitrosti v (modra krožnica na sliki spodaj) lahko razberemo, da morajo biti relativne hitrosti kar velike v primerjavi s svetlobno hitrostjo, da postane dilatacija časa občutna. |
Relativnost simultanosti
Naš stari zdravi razum nam pravi, da se morajo vedno vsi opazovalci strinjati, če se dva dogodka dogodita istočasno, ali če se en dogodek zgodi pred drugim. Recimo, da vidiš dve jabolki – eno rdečo in drugo zeleno – pasti z dveh različnih dreves in hkrati zadeti tla. Seveda boš predpostavil, da ju vsakdo vidi trčiti ob tla istočasno. Če vidiš zeleno jabolko pasti pred rdečim, boš zelo presenečen, če ti bi kdo sporočil, da je videl najprej pasti rdeče. Pripravi se na presenečenje, saj nas bo naslednji miselni poskus prepričal, da se opazovalci v različnih opazovalnih sistemih ne bodo nujno strinjali o vrstnem redu in simultanosti dogodkov, ki se dogodijo na različnih krajih. Vendar bodi pozoren na dejstvo, da se opazovalci v različnih opazovalnih sistemih vseeno morajo medsebojno strinjati o vrstnem redu dogodkov, ki se dogodijo na istem mestu ob različnih časih.
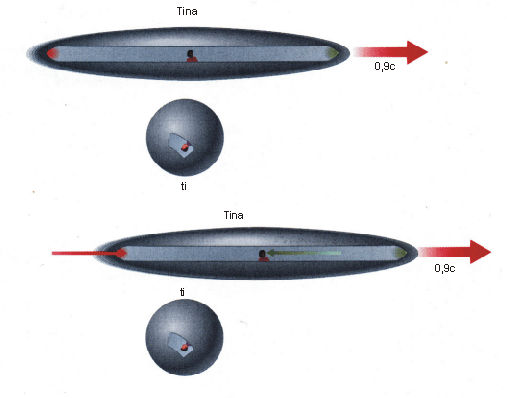
Miselni poskus 8: Tinina dolga ladja ima na začetku in na koncu avtomatska vrata. Tina želi, da se ji oboja vrata med vožnjo mimo tvoje ladje odprejo sočasno. Na vrata zato pritrdi svetlobni senzor, ki vrata odpre takoj, ko nanj pade svetloba. Nato se Tina postavi točno sredino med vrati in hkrati posveti v obe smeri. Ker je razdalja Tine do obojih vrat enaka (stoji namreč na sredini ladje) in hitrost svetlobe absolutna, bo čas leta svetlobe do prvih vrat enak času leta svetlobe do drugih vrat. Oboja vrata se bodo torej za Tino odprla sočasno. Nas pa zanima, če se oboja vrata odprejo sočasno tudi zate, ki Tinino ladjo opazuješ s svoje mirujoče ladje?
Odgovor je ne! Poglejmo zakaj. Ko Tina posveti v smer obojih vrat, se iz svetilke na pot podata dva svetlobna žarka. Ker je svetlobna hitrost enaka za vse opazovalce ne glede na to od kje gledajo svetlobni žarek, potuje svetlobna fronta na obe strani enako hitro tudi zate, ki vidiš Tinino ladjo drveti mimo z veliko hitrostjo. Ker pa se Tina zate premika, bo svetloba prišla do njenih zadnjih vrat prej, kot do sprednjih. Zadnja vrata Tinine ladje se bodo zate odprla prej kot prednja, saj jih bo svetloba dosegla prej, ker ji v tem sistemu ni treba prepotovati celotne razdalje, saj so se ji vrata med tem, ko je potovala, približala. Vrata na začetku ladje pa bo žarek dosegel kasneje, saj se mu sproti odmikajo in jih mora tako loviti.
Če te miselni poskus ni povsem prepričal in si še v dvomih, si lahko ogledaš še en poskus, ki relativnost simultanosti pojasni na malo drugačen način.
Miselni poskus 8a: Tina se ti približuje v novi dolgi vesoljski ladji. Sedi natanko na sredini ladje v kateri je tema. V trenutku, ko je Tina točno ob tebi, na obeh koncih Tinine ladje posvetita svetilki. Po nekaj trenutkih te oba svetlobna žarka s svetilk dosežeta hkrati: zeleni žarek iz začetka Tinine ladje in redči žarek iz konca. Tinina ladja pa se v kratkem času, ko žarka potujeta proti Tininem sedežu, premakne proti točki, kjer si videl, da se je posvetila zelena luč in stran od točke, kjer je posvetila rdeča luč. Zelena svetloba bo dosegla Tino torej pred rdečo, ker je prepotovala krajšo pot. Tino boš tako videl najprej, kako jo osvetli zelena svetloba in nato še rdeča. Tudi sama Tina najprej vidi zeleno luč in šele nato rdečo in se s tabo povsem strinja, da se zanjo zelena luč pojavi pred rdečo. To kar smo povedali do sedaj ni še nič presenetljivega. Vendar se spomnimo, da Tina verjame, da se nahaja točno v središču svoje mirujoče vesoljske ladje. V njenem opazovalnem sistemu potujeta svetlobna žarka iz obeh koncev ladje do nje z enako svetlobno hitrostjo in oba žarka morata prepotovati enako pot. Zato, ker jo zeleni žarek od spredaj doseže pred rdečim od zadaj, mora nujno sklepati, da se je najprej sprožil zeleni blisk in šele nato rdeči nekaj trenutkov kasneje. Tina se s teboj, ko trdiš, da sta se oba bliska sprožila sočasno, ne bi strinjala. Tina upravičeno trdi, da se je zanjo zeleni blisk dogodil pred rdečim.
Učinki na dolžino in maso
Iz dejstva, da teče čas različno v različnih opazovalnih sistemih nujno sledi, da to vpliva tudi na dolžine (ali razdalje) in mase, vendar so razlage tu malo bolj zahtevne. Naslednja dva miselna poskusa uporabljata idejo dilatacije časa, da bi nam pomagala razumeti, kako dilatacija časa vpliva na dolžine in mase.
Miselni poskus 9: Tina se vrne nazaj v svojo prvo vesoljsko ladjo in ponovno drvi tebi nasproti z veliko hitrostjo. Kot ponavadi se z njo strinjaš glede relativne hitrosti, razhajata pa se glede tega, kdo se giblje in kdo miruje. Sedaj si zamisli, da poskuša Tina, med tem ko se giblje mimo, izmeriti dolžino tvoje vesoljske ladje. Kako se loti merjenja? Ker pozna vajino relativno hitrost, lahko preprosto izmeri čas, ki preteče od trenutka, ko skozi okno ob sebi zagleda prednji konec tvoje ladje, do trenutka, ko se mimo odpelje zadnji konec. Dolžina tvoje ladje, ki jo tako izmeri Tina, je preprosto enaka produktu relativne hitrosti ladij in časa, ki ga Tina izmeri za interval med trenutkoma, ko se nahaja ob začetku in ob koncu tvoje ladje. Sam lahko seveda izmeriš dolžino svoje ladje preprosto z metrom. Ker veš, koliko je tvoja ladja dolga in kakšna je relativna hitrost tvoje ladje glede na Tinino, lahko preprosto izračunaš, koliko časa bi moralo trajati potovanje okna Tinine ladje od sprednjega do zadnjega konca tvoje ladje. Točno takšen interval, kot si ga izračunal, izmerijo tudi tvoje ure. Če Tina izmeri enak časovni interval, kakršnega si izračunal, potem vidi tvojo ladjo enako dolgo, kot jo vidiš sam. Vendar se Tinina in tvoja meritev dolžine ladje ne ujemata. Zakaj? Zaradi tega, ker iz svoje ladje vidiš Tinin čas teči počasneje kot svojega! Tinine ure namreč zaradi dilatacije časa izmerijo za isti interval krajši čas. Ker pa je relativna hitrost obeh ladij za oba enaka, torej Tina izračuna za razdaljo med krajem, kjer je sprožila štoparico (prednji konec tvoje ladje) in krajem, kjer je štoparico ustavila (zadnji konec tvoje ladje) krajšo razdaljo, kot si jo izmeril sam.
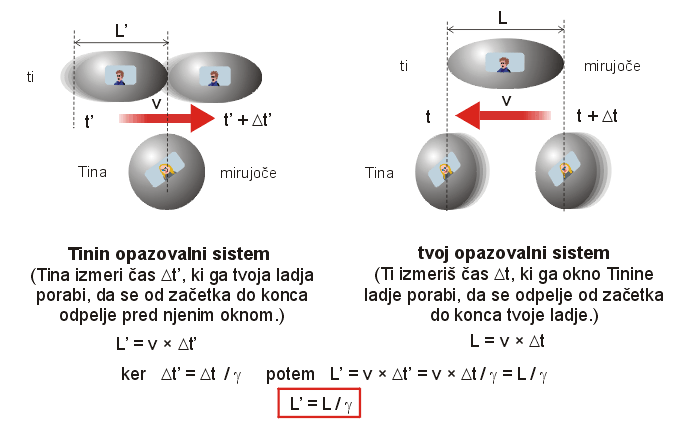
Podobno bi ti izmeril za Tinino ladjo, da je krajša, kot bi bila, če bi mirovala v tvojem opazovalnem sistemu. Temu pojavu pravimo kontrakcija dolžine. Bodi pozoren na dejstvo, da se razdalje skrčijo le v smeri gibanja; ladja je videti krajša, a enako visoka in široka. Če ponovno posplošimo, pridemo do naslednje ugotovitve: iz tvojega gledišča so dolžine predmetov (ali medsebojne razdalje med predmeti), ki se zate gibljejo, krajše v smeri gibanja, kot bi bile, če bi predmet miroval. Hitreje ko se predmet giblje, krajše so razdalje.
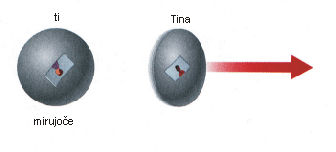
Miselni poskus 10: Zamisli si, da ima Tina sestro dvojčico, ki ji je povsem podobna in ima tudi povsem enako vesoljsko ladjo kot je Tinina. Tinina sestra naj miruje v tvojem opazovalnem sistemu, medtem ko se Tina giblje mimo z veliko hitrostjo. V trenutku, ko Tina pridivja mimo, obe s Tino porineš z enakim sunkom sile. Če sta Tina in njena sestra res povsem podobni, mora imeti sila tvojega potiska enak učinek na obe sestri. Vendar pa, zato ker boš videl Tinin čas teči počasneje, boš sklepal, da čuti Tina tvojo silo krajši čas kot njena sestra. (Če s Tinino sestro izmerita, da je potisk trajal 1 mikrosekundo, potem izmeri Tina, da je potisk trajal manj kot 1 mikrosekundo.) Ker čuti Tina tvojo silo krajši čas kot njena sestra, ima potisk manjši vpliv na njeno hitrost, kot na hitrost njene sestre. Povedano z drugimi besedami: tvoj potisk ima manjši vpliv na Tino kot na njeno sestro, ne glede na to, da si obe porinili z enako silo. Po Newtonovih zakonih gibanja, je edina možna razlaga, da bi imela enaka sila različen učinek na Tino in njeno sestro v tem, da je Tinina masa večja, kot je masa njene sestre. Ta pojav je znan kot povečanje mase. Posplošeno povedano: iz tvojega gledišča imajo predmeti, ki se glede nate gibljejo, večjo maso, kot bi jo imeli, če bi mirovali. Hitreje, ko se objekt giblje, večja je njegova masa.
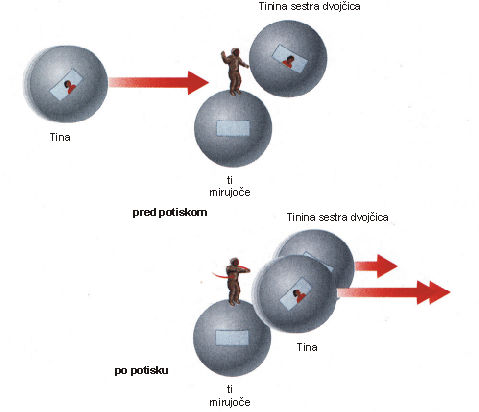
S povečevanjem mase si lahko na nov način pojasnimo tudi, zakaj snov ne more doseči svetlobne hitrosti. Hitreje, ko se predmet giblje, večjo maso mu boš izmeril. Pri velikih hitrostih bo imela enaka sila manjši učinek na hitrost predmeta. Ko se hitrost predmeta približuje svetlobni hitrosti, se bo njegova masa povečevala preko vseh meja. Ker ni sile, ki bi lahko pospešila neskončno veliko maso, ne bo predmet nikoli uspel pridobiti tistega zadnjega povečanja hitrosti, ki bi mu omogočil, da bi se gibal s hitrostjo svetlobe.
Seštevanje hitrosti
Ogledati si moramo še en zelo pomemben pojav. V naslednjem miselnem poskusu se s Tino ne boš mogel strinjati glede hitrosti snovnih teles, ki se gibljejo relativno druga na drugo. Strinjal se boš le o hitrosti svetlobe.
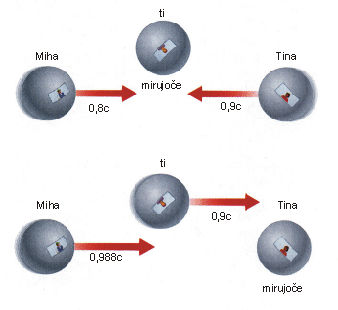
Miselni poskus 11: Tina se ti približuje s hitrostjo 0,9c. Tvoj prijatelj Miha skoči v svojo vesoljsko ladja in se odpelje Tini nasproti s hitrostjo 0,8c (to je hitrost, ki jo ti izmeriš). Vprašanje, ki nas zanima je: kako hitro ga bi videla prihajati Tina? Zdravorazumsko bi Tina morala videti Miho, kako prihaja proti njej s hitrostjo 0,9c + 0,8c = 1,7c. Vendar sedaj že vemo, da je ta odgovor napačen, ker je 1,7c hitreje od svetlobe hitrosti. Tina mora videti, da se ji Miha približuje s hitrostjo, ki je manjša od c, vendar s hitrostjo, ki je večja on 0,9c, s katero se ji približujete ti. Zaključila bo torej, da je Mihova hitrost nekje med 0,9c in c (točna vrednost, ki jo dobimo z računom je 0,988c).
Kaj je pravzaprav resnično?
“Poskušamo si čim hitreje dokazati, da se motimo, kajti le tako lahko uspemo napredovati.” (Richard Feynman)
Pokazali smo, kako sledijo vse velike napovedo teorije relativnosti neposredno iz absolutnosti hitrosti svetlobe in dejstva, da so zakoni narave enaki za vse opazovalce. Čeprav je bila logika naših miselnih poskusov zelo preprosta, so napovedi resnične šele, ko jih podpremo tudi z opazovanji ali empiričnimi poskusi. So torej nenavadne napovedi relativnosti resnične? Najprej si oglejmo zgodovino meritev svetlobne hitrosti, potem pa še nekaj poskusov, na podlagi katerih lahko sklepamo, da svetloba ne potuje s konstantno hitrostjo c le v enem posebej izbranem opazovalnem sistemu, ampak v vseh sistemih.
Zgodovina meritev hitrosti svetlobe
Že Galileo Galilei je domneval, da ima svetloba končno hitrost, a je za časa svojega življenja na žalost ni uspel izmeriti, čeprav je to prvi tudi praktično poskušal. Poskus je načrtoval takole: pomočnik z zaslonjeno svetilko na bližnjem griču naj bi odstrl svojo svetilko, potem ko bi zagledal svetilko, ki jo je odstrl Galilei ob vznožju griča. Na ta način bi Galilei lahko izmeril čas, ki ga je svetloba potrebovala za pot do vrha griča in nazaj. Poskus je večkrat ponovil, a iz izida je lahko sklepal le, da je čas potovanja svetlobe veliko krajši, kot je odzivni čas človeka na svetlobni dražljaj. Da hitrost svetlobe ni neskončna, je nekaj desetletij po Galileijevi smrti prvi pokazal mladi danski astronom Ole Romer, ki je takrat delal v pariški zvezdarni. V sedemdesetih letih 17. stoletja je opazoval zakasnitve mrkov Jupitrove lune Io. Opazil je, da si mrki ne sledijo v enakih časovnih razmikih, ampak da za malenkost prehitevajo izračunane napovedi v obdobju, ko se Zemlja giblje proti Jupitru, in malenkostno zaostajajo, ko se Zemlja od Jupitra oddaljuje. Po večletnih meritvah je ocenil, da znaša zakasnitev mrkom med trenutkom, ko je Zemlja najbliže Jupitru in trenutkom, ko je Zemlja najdlje, 22 minut. O svojem odkritju je napisal obširno razpravo v kateri je pokazal, da se teh zakasnitev ne da pojasniti drugače kot s sklepom, da ima svetloba končno in ne neskončno hitrost. Vendar strokovne javnosti ni uspel takoj prepričati. Znani astronom Cassini, ki je bil takrat njegov šef v pariški zvezdarni, se z Romerjevo interpretacijo ni strinjal, idejo pa sta takoj podprla Huygens in Newton. Zanimivo pa je, da v nasprotju s tem kar piše v večini učbenikov fizike in astronomije, sam Romer ni nikoli poskušal natančno izračunati hitrosti svetlobe. Dovolj mu je bilo že, da je dokazal, da hitrost ni neskončna. Zapisal je le oceno, da porabi svetloba manj kot sekundo, da prepotuje razdaljo enako enemu zemeljskemu premeru, kar v številkah pomeni, da je hitrost svetlobe večja kot 12.000 km/s.
Zvezdna aberacija
Po povsem drugi poti je do ocene hitrosti svetlobe prišel angleški astronom James Bradley v sredini 18. stoletja. Uporabil je t.i. “dežno” metodo. Kako je razmišljal? Če se ne želim zmočiti, ko hitro hodim po dežju, moram dežnik nagniti malo naprej. Takrat se mi zdi, kot da deževne kapljice prihajajo iz poševne (navidezne) smeri, ki je od navpične (prave) nekoliko odklonjena. Še lepše lahko ta pojav opazujem, ko se skozi dež vozim z avtomobilom. Kaj pa, če namesto dežja “pada” svetloba. Namesto dežne kapljice si predstavljajmo svetlobno “kapljico” ali foton, ki se giblje s svetlobno hitrostjo, namesto dežnika pa daljnogled. Podobno kot dežnik med hojo po dežju, mora tudi gibajoči se astronom malo nagniti daljnogled naprej od prave smeri zvezde, da jo lahko opazuje. Zemlja kroži okoli Sonca s hitrostjo 30 km/s in smer te hitrosti se stalno spreminja, tako da se v enem letu, ko Zemlja zaključi en obhod okoli Sonca, spremeni ravno za 360°. Zato navidezna smer zvezde, ki se nahaja blizu nebesnega pola, ves čas “pleše” po elipsi okoli prave smeri. Zvezdno aberacijo lahko opazimo samo z daljnogledi, saj znaša največji odmik le okoli tretjino kotne minute, ločljivost človeškega očesa pa je okoli ene kotne minuta. Če poznamo kot med navidezno in pravo smerjo proti zvezdi, in hitrost našega gibanja, lahko s preprosto enačbo ocenimo hitrost svetlobe. Bradleyevo odkritje zvezdne aberacije je dodalo tudi pomemben argument k dokazu za gibanje Zemlje okoli Sonca in potrdilo heliocentrični sistem.
In kakšen pomen ima Bradleyevo odkritje za teorijo relativnosti? Ko so v 19. stoletju spoznali, da je svetloba elektromagnetno valovanje, se je zastavilo vprašanje, kaj je medij tega valovanja. Kot je zvok valovanje zraka, so za medij svetlobe določili eter, vendar nihče ni prav dobro vedel, kaj to je. Zaradi zvezdne aberacije so lahko le sklepali, da se Zemlja glede na eter giblje, saj v primeru, da bi Zemlja glede na eter mirovala, aberacije ne bi opazili, ker bi nam svetlobni dež padal navpično na glavo.
Michelson-Morleyev poskus
Ob koncu 19. stoletja se je mladi asistent fizike Albert A. Michelson lotil poskusa, s katerim je poskušal natančno izmeriti hitrost Zemlje ob potovanju skozi eter. V ta namen je razvil zelo natančni instrument, ki se danes po njem imenuje Michelsonov interferometer. V njem enobarvni svetlobni curek pade na polprepustno ploščico v sredini (glej sliko!). Valovanje ploščica delno prepusti, delno pa ga pod kotom 90° odbije. Obe delni valovanji se na ravnih zrcalih zgoraj in desno odbijeta in ponovno sestaneta na polprepustni ploščici, interferenčno sliko pa opazujemo z daljnogledom. Zgornje zrcalo je gibljivo z mikrometrskim vijakom v smeri valovanja. Če bi bila oba kraka interferometra enako dolga, bi bilo vidno polje interferometra temno, ker bi se valovanji svetlobe iz obeh krakov ob ponovni združitvi ravno izničili. Črno piko bi videli tudi, če bi bila razlika dolžine krakov cel večkratnik valovne dolžine svetlobe, ki jo uporabljamo. Vidno polje bi bilo svetlo, če bi bila razlika dolžine krakov lih večkratnik polovične valovne dolžine, saj bi to pomenilo, da se curka iz obeh krakov ob združitvi koherentno ojačita. Ker curek vsebuje tudi delna valovanja z nekoliko drugačnim nagibom, opazimo v vidnem polju svetle in temne kolobarje, ki lezejo iz sredine, ko narašča razlika med dolžino krakov. Michelsonov interferometer je v bistvu naprava, za zelo natančno merjenje razdalj. Na nekaj sto nanometrov natančno lahko namreč izmerimo razdaljo, za katero smo podaljšali enega od krakov, če preštejemo kolobarje, ki nastanejo na novo.
Če obstaja eter kot nosilec elektromagnetnega valovanja, se Zemlja v njem giblje. To dokazuje zvezdna aberacija. Hitrost svetlobe na Zemlji je tedaj odvisna od smeri in velikosti hitrosti Zemlje v etru. Hitrost Zemlje pri gibanju okoli Sonca je 30 km/s, zato bi se morala hitrost svetlobe zaradi vrtenja Zemlje spremeniti vsaj za dvakrat toliko. Vzemimo, da kaže en krak interferometra v smeri gibanja Zemlje po etru. Po tem kraku potuje svetloba najprej proti etru in nato z njim in porabi za potovanje do zrcala in nazaj določen čas, ki ga lahko izračunamo, če poznamo hitrost potovanja Zemlje skozi eter, hitrost svetlobe in dolžino kraka. Prav tako lahko izračunamo tudi čas, ki ga curek potrebuje za potovanje po kraku pravokotno na smer gibanja Zemlje v etru. Razlika obeh časov je v tesni povezavi s progami, ki jih vidimo v interferometru. Če namreč kraka zasukamo za 90°, ravno zamenjata tudi usmerjenost gibanja glede na eter. Ker sta časa potovanja obeh curkov po krakih odvisna od usmerjenosti glede na eter, bi morali med sukanjem interferometra zaznati premike interferenčnih prog. Premik bi moral biti odvisen od kvadrata hitrosti potovanja Zemlje skozi eter:
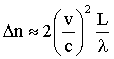
Kljub temu, da se je zelo trudil in izgradil natančen inštrument, Michelsonu ni uspelo izmeriti nikakršnega gibanja. Za poskus je navdušil še starejšega kolega kemika E. W. Morely, a tudi z njegovo pomočjo in s še bolj izpopolnjenim interferometrom nista uspela izmeriti nikakršnega gibanja. Pri prvem poskusu leta 1881 je Michelsonovem pričakoval premik za 0,03 razmika med sosednjima progama, pri drugem Michelson-Morleyevem poskusu leta 1886 pa premik 0,4. Toda, kljub dovolj dobri natančnosti, ni bilo mogoče opaziti nobenega premika interferenčnih prog. Kaj to pomeni? Aberacija po eni strani pravi, da se glede na eter gibljemo, Michelson-Morleyev poskus pa, da glede na eter mirujemo (glej tudi tekst Michelson-Morleyev poskus).
To neskladje je pravilno pojasnil šele Einstein s posebno teorijo relativnosti. Če vpeljemo načelo, da je hitrost svetlobe v praznem prostoru konstanta, ki je neodvisna od gibanja svetila in opazovalca, težav ni več. Einstein je pokazal, da ni potrebe, da bi vpeljali posebej odlikovani opazovalni sistem, v katerem ima svetloba hitrost c v drugih, ki se gibljejo glede nanj, pa drugačno. Ali z drugimi besedami povedano: etra ni! Seveda pa je cena, ki jo moramo za to spoznanje plačati, ugotovitev, da Newtonova mehanika ni dovolj splošna, da bi opisovala tudi dogajanje pri velikih hitrostih v primerjavi s hitrostjo svetlobe.
Eksperimentalne potrditve dilatacije časa
Čeprav (trenutno) še ne moremo potovati s hitrostmi, pri katerih bi bili učinki relativnosti pomembni, lahko majhni subatomski delci te hitrosti dosežejo velikokrat. V pospeševalnikih delcev fiziki pospešujejo subatomske delce do hitrosti, ki so zelo blizu svetlobne hitrosti, in nato opazujejo, kaj se dogaja, ko delci trčijo. Pri takem trku se lahko kinetična energija, ki jo nosijo hitri delci, pretvori v energijo mase, kar sproži pravi plaz nastajanja novih delcev. Veliko teh delcev ima zelo kratko življenjsko dobo, tako da hitro razpadejo v druge, bolj stabilne delce. Delec z imenom pi+ mezon ima življenjsko dobo približno 18 nanosekund, ko miruje. Pi+ mezoni, ki pa se po nastanku gibljejo s hitrostjo blizu svetlobne hitrosti, živijo v povprečju veliko dlje kot 18 nanosekund, natanko tako, kot predvideva formula za dilatacijo časa. S pospeševalniki delcev se lahko prepričamo tudi o dejstvu, da nič snovnega ne more doseči svetlobne hitrosti. V pospeševalniku je razmeroma preprosto pospešiti delce do hitrosti 0,99c. Vendar se nato, ne glede na to, koliko dodamo nove energije, delcem hitrost poveča le za malenkost. Nekateri pospeševalniki so delce pospešili že do hitrosti 0,00001% svetlobne hitrosti, a doseči je ni uspel še nihče.
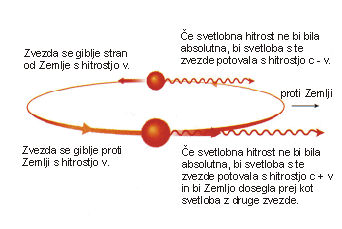
Čeprav so učinki relativnosti očitni šele pri velikih hitrostih, so moderne naprave za merjenje časa že tako natančne, da lahko izmerijo učinke dilatacije časa že pri običajnih hitrostih. Leta 1975 so v nekem poskusu primerjali tek ure, ki je potovala z letalom, z drugo uro, ki je mirovala na tleh. V 15 urah poleta so ure na letalu izgubile 6 nanosekund v primerjavi z urami na tleh, kar se je skladalo z napovedmi teorije relativnosti. Da je svetlobna hitrost absolutna, se lahko prepričamo tudi z opazovanjem dvojne zvezde. Če svetlobna hitrost ne bi bila absolutna, bi imela svetloba z zvezde, ko se ta giblje v naši smeri večjo hitrost, kot takrat, ko se od nas oddaljuje. V določenih primerih bi se npr. lahko zgodilo, da bi videli isto zvezdo na dveh mestih hkrati, ker bi nas hitrejša svetloba iz prve točke dosegla hkrati kot počasnejša svetloba iz druge točke, kjer je bila zvezda prej. Tega pojava astronomi še nikoli niso opazili.
Pot k novi predstavi narave
“Potreben je zelo neobičajen um, da se loti analize očitnega.” (Alfred North Whitehead)
Z miselnimi poskusi smo pokazali, da naš stari zdravi razum pri relativnosti ne deluje, potem pa smo si ogledali, kako resnični empirični poskusi podpirajo dognanja naših miselnih poskusov. Nismo pa še ugotovili, kakšna nova predstava dogajanja v naravi bi lahko nadomestila stari zdravi razum. Še en miselni poskus nam bo pokazal, da je vse skupaj še bolj čudno, kot smo si do sedaj predstavljali.
Miselni poskus 12: Zamisli si, da Tina potuje mimo tvoje ladje s hitrostjo, ki je blizu hitrosti svetlobe. Iz prejšnjih miselnih poskusov vemo, da boš videl njen čas teči počasneje, dolžina njene ladje bo krajša, masa pa povečana. Zanima nas, kaj bi o tebi rekla Tina? Njej se seveda zdi, da ona sama ne potuje nikamor; zanjo se z veliko hitrostjo giblješ ti. Ker so zakoni narave za vse enaki, mora tudi ona priti do enakih zaključkov, do katerih si ti prišel tudi ti. Ugotovila bo, da tvoj čas teče počasneje, da je dolžina tvoje ladje krajša in tvoja masa povečana!
Naleteli smo na zapleten problem. Zamisli si, da imaš močan teleskop, ki ti omogoča, da lahko skozi okno ves čas opazuješ, kaj se dogaja v Tinini ladji. Opaziš, da se vse dogaja kot v počasnem posnetku. Tini pošlješ radijsko sporočilo: “Zdravo Tina! Zakaj se premikaš tako počasi?” Ker potuje radijsko sporočilo s svetlobno hitrostjo, ga Tina brez težav sprejme, in nato odgovori s svojim sporočilom. Ko poslušaš njen odgovor, ga slišiš seveda kot v počasnem posnetku: “Zdddrrrraaaavvvvooooo…” kar te prepriča, da njen čas res teče počasneje. Vendar pa, ko sprejmeš celotno sporočilo in z računalnikom naravnaš hitrost njenega govora na normalno, zaslišiš Tinino sporočilo: “Jaz se že ne gibljem kot v počasnem posnetku, ti se giblješ počasi!”
Lahko se pritožiš Tini in ona nazaj tebi, a pogovor ne vodi nikamor. Nato pa te prešine izvrstna ideja. Dogajanje v Tinini sobi boš posnel s pomočjo teleskopa na video kamero in poslal posnetke Tini. Na posnetku se lepo vidi, da Tinina ura teče počasneje kot tvoja. Video kaseto daš v zelo hitro poštno vesoljsko ladjo in jo pošlješ Tini. Ko si bo ogledala kaseto, se bo prepričala, da počasneje teče njen čas in ne tvoj. Preden pa zmagoslavno razglasiš, da si Tino končno prepričal, se pojavi še ena težava. Tudi Tina je prišla do enake ideje in ravnokar si prejel njeno pošto z videokaseto, na kateri je Tina skozi svoj teleskop posnela tvojo vesoljsko ladjo. Ko si posnetek na Tinini kaseti ogledaš, ugotoviš da ima tudi Tina prav; tvoj čas res teče zanjo počasneje od njenega.
Kako to, da lahko ti vidiš Tinine ure teči počasneje, Tina pa tvoje? Pomisli na našo razpravo o pojmih zgoraj in spodaj in o telefonskem pogovoru Avstralca in Evropejca. Oba se lahko noč in dan prepirata, kdaj je Luna spodaj in kdaj zgoraj. Ko pa enkrat določimo pojme zgoraj in spodaj glede na središče Zemlje, nesporazumov ni več. Na enak način pride tudi do tvojega nesporazuma s Tino, ker oba razmišljata o prostoru in času na stari način, ki pravi, da sta prostor in čas absolutna, hitrost svetlobe pa relativna. Teorija relativnosti postavi to intuitivno prepričanje na glavo. Absolutna je svetlobna hitrost, prostor in čas pa sta relativna. Nekdo, ki je sprejel novo relativistično predstavo narave, ne bi bil nad tvojim nesporazumom s Tino nič bolj presenečen, kot smo mi danes nad pogovorom Avstralca in Evropejca o tem, kaj je zgoraj in kaj spodaj. Vajin spor je neosnovan, ker temelji na neustrezni definiciji prostora in časa. Kar šteje so opazovanja in rezultati poskusov in vsak tvoj poskus bo imel enake rezultate kot Tinin. Za oba veljajo isti zakoni narave, ki pa niso povsem skladni z našim starim intuitivnim občutkom za dogajanje v naravi.

Vozovnica k zvezdam
Iz dejstva, da hitrosti svetlobe ne moremo doseči, bi lahko sklepali, da so oddaljene zvezde povsem izven našega dosega. Vendar nam dilatacija časa in kontrakcija dolžine omogočata, da si vseeno lahko kupimo vozovnico k zvezdam, če bomo le kdaj sposobni izgraditi vesoljsko ladjo, ki bi potovala s hitrostjo, ki je blizu svetlobni hitrosti.
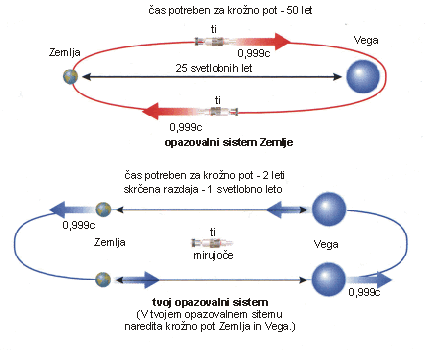
Miselni poskus 13: Zamisli si, da bi šel na pot do zvezde Vega, ki je oddaljena 25 svetlobnih let. Na voljo imaš ladjo, ki lahko potuje s hitrostjo 0,999c. Potovanje bi za opazovalca na Zemlji trajalo približno 25 let, saj potuješ skorajda s svetlobno hitrostjo, razdalja pa je 25 svetlobnih let, in prav toliko še za vrnitev. Če odpotuješ recimo leta 2025, bi Vego dosegel leta 2050, na Zemljo pa bi se vrnil leta 2075. Iz tvojega opazovalnega sistema pa se ti zdi, da ostajaš na mestu, s hitrostjo 0,999c pa se oddaljuje Zemlja in približuje Vega. Zato se ti bo razdalja med Zemljo in Vego iz 25 svetlobnih let skrčila na nekaj več kot 1 svetlobno leto. Ker se ti Vega približuje s hitrostjo 0,999c, razdalja do Vege pa je zate le 1 svetlobno leto, bo potovanje do Vege zate trajalo le 1 leto. Nazaj boš prav tako potoval le eno leto, zato bodo tvoje ure izmerile za celotno pot le 2 leti. Če boš ob odhodu star 30 let, se boš vrnil star 32 let. Čeprav se zdijo naše ugotovitve nenavadne, sta oba pogleda na potovanje prava. Če odpotuješ z Zemlje leta 2025, ko si star 30 let, se boš vrnil leta 2075, ko boš star 32 let. Čeprav se boš med potjo postaral le za 2 leti, bodo tvoji prijatelji na Zemlji ob povratku starejši kar za 50 let.
Načrtoval pa bi lahko tudi daljše polete na bolj oddaljene zvezde v vesolju, če bi le imel dovolj hitro ladjo. Andromedina galaksija je oddaljena 2,5 milijonov svetlobnih let, kar pomeni, da bi pot do nje in nazaj za opazovalca na Zemlji trajala 5 milijonov let. Vendar pa bi, če bi le uspel potovati s hitrostjo, ki je že zelo blizu svetlobni hitrosti [ npr. (1-5*10-11)c ], bi zate celotno potovanje trajalo le 50 let. Če bi Zemljo zapustil za svoj 30-ti rojstni dan, se bi vrnil star 80 let, pri čemer bi ob povratku našel le še ostanke našega sončnega sistema, vsi prijatelji in vse kar ti je bilo znano, pa bi izginilo že pred 5 milijoni let (glej tudi: Razrešitev paradoksa dvojčkov).
Če gledamo skozi čas, nam da relativnost pravzaprav le enosmerno vozovnico k zvezdam. Lahko se podamo na pot in obiščemo zvezde, a nikoli več se ne bomo mogel vrniti v dobo, v kateri smo se na potovanje podali.
Priredba poglavja o relativnosti iz knjige The Cosmic Perspective, 1999.


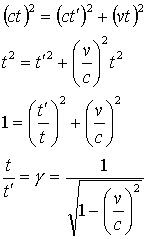














Koncept časovne indukcije posega v območje negativne energije. Ko uspemo vzdrževati mejo Casimirjevega področja na površini telesa . npr krogle lahko vloženo pozitivno energijo v notranjosti, ki je pretvorjena v negativno pojmujemo kot presežek časa v zlomljeni simetriji.
Z nihanjem tega razmerja v sinusni maniri zanihamo čas na Casimirjevi meji. Z ojačanjem tega pojava, ki povzroči širjenje meje Casimirjevega območja lahko ,če vstopimo v to območje gibljemo v času. Torej Čas je harmonična veličina z morebitnimi vsemi višje harmonskimi komponentami.
https://arxiv.org/pdf/physics/9805038.pdf