Je gravitacija skrivnostna sila, ki deluje na daljavo med masnimi telesi? Einsteinova splošna teorija relativnosti pravi, da ni gravitacija nič skrivnostnega, ampak je le odsev ukrivljenosti prostora-časa.
Einsteinova druga revolucija v dojemanju prostora in časa
Nemogoče si je predstavljati štiridimenzionalni prostor. Sam imam dovolj problemov že s predstavami v treh dimenzijah. (Stephen Hawking)
Zamisli si, da živiš v dobi, ko vsi ljudje verjamejo, da je Zemlja ravna ploskev. Kot bogat mecen znanosti, organiziraš odpravo v najbolj oddaljene dele sveta. Izbereš dva neustrašna raziskovalca in jima daš natančna navodila: ves čas morata hoditi povsem naravnost. Opremiš ju tako, da lahko potujeta po kopnem in po vodi. Ob slovesu ju postaviš s hrbti skupaj in poskrbiš, da odkorakata v smereh, ki se razlikujeta ravno za 180 stopinj. Takrat jima tudi naročiš, naj se vrneta šele, ko odkrijeta kaj zelo nenavadnega. Ko preteče nekaj časa, se popotnika vrneta domov in poročata, da sta res odkrila nekaj neobičajnega. Po nekaj letih se vrneta in ti poročata, da sta res doživela nekaj zelo nenavadnega. Čeprav sta ves čas hodila povsem naravnost v nasprotne strani, sta se vseeno srečala v neki tuji deželi, kar ju je zelo presenetilo. To je bilo zanju, ki sta verjela, da je Zemlja ravna ploskev, res nekaj nepojmljivega, a za nas, ki vemo, da je Zemlja okrogla, težav v tej dogodivščini ni. Čeprav sta popotnika hodila res ves čas naravnost, je njuna ravna pot še zmeraj sledila krivini Zemlje, kar je povzročilo, da sta se srečala na drugem koncu našega planeta.
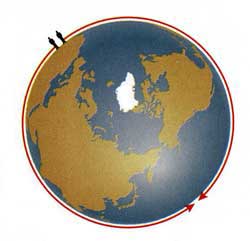
Sedaj pa si zamislimo še en sodobnejši scenarij. Nekje v vesolju prosto lebdiš v vesoljski ladji. Da bi raziskal prostor v okolici, pošlješ v nasprotni strani dve mali sondi. Vsaka sonda ima vgrajeno kamero, ki pošilja sliko nazaj na tvojo ladjo. Predstavljal si, da na ekranu potem, ko sta sondi že zelo daleč vsaka v svoji smeri naenkrat zagledaš, kako lahko s kamero prve sonde spet vidiš drugo in s kamero druge prvo. Čeprav si sondi poslal vsako v ravno nasprotno smer in nista imeli vgrajenih motorjev, sta se vseeno srečali. Kako je to mogoče?
Od Newtona naprej si ponavadi pojasnimo ukrivljene poti sond kot posledico gravitacijske sile. Ali ne bi mogli po analogiji z raziskovalci, ki so se srečali na nasprotni strani Zemljinega površja, sklepati tudi, da se sondi ponovno srečata, ker je prostor zakrivljen? Ideja, da je lahko prostor ukrivljen, se morda na začetku sliši nenavadno. Čeprav si lahko predstavljamo, kako se površina ukrivi v prostoru, si naše predstavne zmožnosti ne morijo predočiti tridimenzionalnega prostora, ki bi bil ukrivljen. Ideja, da je prostor lahko ukrivljen, je temelj Einsteinove druge revolucije oz. splošne teorije relativnosti iz leta 1915, ki je prinesla nov pogled na gravitacijo.

Že iz posebne teorije relativnosti vemo, da sta prostor in čas nerazdružljivo povezana. Tri dimenzije prostora in ena dimenzija časa tvorijo sedaj štiridimenzionalno mešanico, ki ji pravimo prostor-čas. Splošna teorija relativnosti pravi, da snov oblikuje prostor-čas podobno, kot uteži deformirajo napeto ponjavo. Seveda ne moremo postaviti uteži na prostor-čas, ker vsa snov obstoji le znotraj prostora-časa, hkrati pa si deformacije prostora-časa tudi ne moremo predstavljati. S prispodobo uteži na ponjavi si lahko le pomagamo pri spoznavanju načel splošne relativnosti, ki urejajo strukturo prostora-časa.
Naštejmo nekaj idej, ki sledijo neposredno iz Einsteinove splošne teorije relativnosti:
- Gravitacija je posledica deformacij prostora-časa in ni neka skrivnostna sila, ki deluje na daljavo. Deformacije nastanejo zaradi prisotnosti mase in določajo, kako se bodo drugi predmeti gibali skozi prostor-čas.
- V gravitacijskem polju teče čas počasneje. Močnejša je gravitacija, počasneje teče čas.
- V prostoru-času lahko nastanejo črne luknje, s padcem v katero snov zapusti opazljivo vesolje.
- Vesolje nima ne roba ne središča, čeprav je mogoče, da ima vseeno končno velik volumen.
- Velike mase, ki se hitro premikajo, oddajajo gravitacijske valove, ki potujejo s svetlobno hitrostjo.
Načelo ekvivalentnosti
Posebna teorija relativnosti je pokazala, da ni enoznačnega odgovora na vprašanje: “Kdo se pravzaprav giblje?”, ko potujeta dve osebi relativno ena na drugo s konstantno hitrostjo. Obe osebi lahko enako upravičeno trdita, da mirujeta ali da se premikata. Vendar pa situacija postane s trenutkom, ko v igro vstopi pospešeno gibanje, bolj zapletena.
Zamisli si, da s prijateljico Tino prosto lebdita v breztežnosti vsak v svoji vesoljski ladji, ko se na tvoji ladji vžgejo motorji. Tina opazi, da se od nje pospešeno oddaljuješ, zato ti pošlje sporočilo: “Lep pozdrav in srečno pot!” Tebi se nasprotno dozdeva, da se pospešeno oddaljuje pravzaprav Tina, zato ji odgovoriš: “Hvala, ampak jaz ne potujem nikamor. Ti si tista, ki potuješ stran.” Vendar se kmalu izkaže, da tvoje sporočilo ni povsem na mestu. Če bi se gibal s konstantno hitrostjo glede na Tino, bi oba prosto lebdela in tako ne bi bilo mogoče ugotoviti, kdo se pravzaprav giblje. Vendar zaradi pospeševanja ti občutiš silo, ki te pritisne k tlom, medtem ko Tina še naprej prosto lebdi v svoji ladji. Če se tvoja ladja pospešuje s pospeškom 9,8 m/s2, kar je enako težnemu pospešku na Zemlji, potem se ti bo zdelo, kot da si doma na Zemlji in ne v vesolju. Tako ti Tina lahko odpiše: “Če že trdiš, da ne potuješ nikamor, kako to, da si pritisnjen k tlom svoje ladje in zakaj imaš vklopljene motorje? Zakaj pa jaz ne čutim nobene sile, če se res pospešujem?”
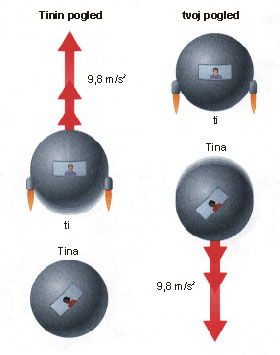
Priznati moraš, da Tina postavlja res dobra vprašanja. Vse kaže, da si ti tisti, ki se giblješ in da nimaš več možnosti, da bi Tino prepričal o nasprotnem. Vendar Einstein ni maral takšnih situacij, ker je verjel, da je vse gibanje le relativno. Leta 1907 se mu je utrnila ideja, ki jo je kasneje imenoval: “najsrečnejša misel mojega življenja.” Razodetje mu je prineslo spoznanje, da lahko vedno, ko občutimo težo (kot nasprotje breztežnosti), njen vzrok pripišemo enako utemeljeno ali gravitaciji ali pospeševanju. Ideja se imenuje načelo ekvivalentnosti in se bolj točno glasi: učinki gravitacije so ekvivalentni učinkom pospeševanja. (Če smo povsem natančni, moramo dodati, da to velja samo za zelo male delčke prostora, ker lahko v večjih območjih prostora gravitacija povzroči tudi plimne sile, pospeševanje pa jih ne more.)
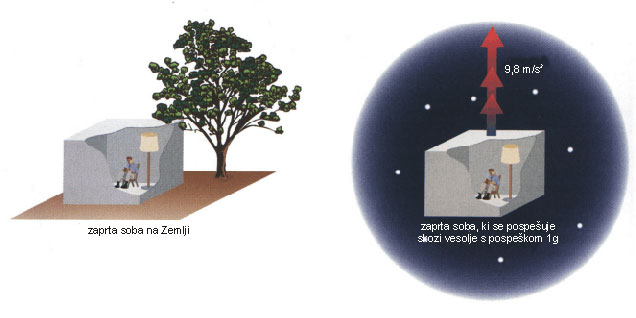
Da bi si lažje predstavljal pomen načela ekvivalentnosti, si zamisli, da sediš v naslonjaču v sobi z zastrtimi okni in vrati. Tvoja soba ne nato skrivnostno odlepi od Zemlje in začne potovati po vesolju s pospeškom 9,8 m/s2 oz. 1g. Po načelu ekvivalentnosti, znotraj sobe nikakor ne moreš ugotoviti, da nisi več na Zemlji. Katerikoli poskus izvedeš, zmeraj boš dobil enake rezultate, kot na Zemlji.
Sedaj se vrnimo nazaj k Tini, ki je trdila, da se moraš ti pospeševati, ker le ti občutiš težo v svoji vesoljski ladji. Po načelu ekvivalentnosti lahko sedaj enako utemeljeno trdiš, da je tvoja teža posledica gravitacije. Po tej razlagi je prostor okoli tvoje ladje v gravitacijskem polju, ki kaže navzdol k zadnjemu delu ladje. Miruješ le zaradi tega, ker ti raketni motorji na ladji omogočajo, da lebdiš in na padeš navzdol, podobno kot oseba, ki nad površjem Zemlje lebdi v helikopterju in tudi občuti težo. Tina pa nasprotno, ker ni vžgala motorjev, prosto pada v gravitacijskem polju. Vsakdo, ki prosto pada, pa teže ne čuti in zdi se mu, da je v breztežnosti. Situacija je podobna, kot da bi ti uspel lebdeti ob previsni steni, medtem ko bi Tina padala v globino. Sedaj ji lahko mirno odgovoriš: “Žal mi je Tina, vendar jaz še zmeraj trdim, da mirujem. Motorje sem uporabil le, da sem preprečil padanje, težo pa čutim zaradi gravitacije. Ti pa čutiš breztežnost, ker prosto padaš. Upam, da se ne boš poškodovala, ko boš dosegla tla oz. karkoli že leži na dnu tega gravitacijskega polja.”
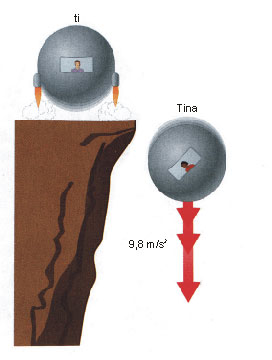
Z načelom ekvivalentnosti lahko trdimo, da je vse gibanje relativno. To načelo je vstopna točka v splošno teorijo relativnosti. Enako, kot smo izpeljali nenavadne posledice posebne teorije relativnosti iz ideje, da je svetlobna hitrost absolutna, sledi splošna teorija relativnosti iz načela ekvivalentnosti. Podobno kot nam je posebna relativnost razkrila nekaj novih resnic o naravi (npr. da sta prostor in čas različna za opazovalcev različnih opazovalnih sistemih), nam bo splošna relativnost pokazala celotno vesolje v povsem novi luči.
Kako razumeti prostor-čas?
Lahko je reči, da lahko občutek teže pripišemo enakovredno učinku gravitacije ali pospeševanja, težje pa si je vse to predstavljati. Osebo, ki stoji na površini Zemlje, npr. vidimo mirovati, medtem ko astronavt, ki se pospešeno giblje skozi prostor, neprestano povečuje svojo hitrost. Kako lahko gravitacija in pospeševanje povzročata enake učinke, ko pa izgledata tako različno? Po splošni teoriji relativnosti je ta navidezna različnost le posledica naše nezmožnosti, da bi pojave gledali v štiridimenzionalnem prostoru-času.
Štiri razsežnosti
Pod pojmom razsežnost (dimenzija) običajno razumemo število neodvisnih smeri prostora, v katerih je mogoče gibanje. Točka ima tako razsežnost nič, saj bitja ujeta v točki nimajo nobene svobode gibanja. Enorazsežna gibanja so gibanja po črti, ker imamo na črti le eno možno smer gibanja, po kateri lahko hodimo naprej ali nazaj. Če imamo na voljo dve neodvisni smeri gibanja, se nahajamo na ploskvi oz. v dvorazsežnem svetu, pri treh neodvisnih smereh pa smo v trirazsežnem prostoru. Prostor v katerem živimo je trirazsežen, vendar iz dejstva, da višjih dimenzij ne vidimo in se v njih ne moremo gibati, še ne moremo sklepati, da mogoče vseeno ne obstajajo. Vsaj matematično jih ni težko opisati, saj lahko običajnim trem prostorskim koordinatam dodamo še nove. Prostorom, ki so več kot trirazsežni pravimo hiperprostori.
Prostor-čas
Prostor-čas primer je štirirazsežnega prostora v katerem so štiri smeri možnega gibanja po dolžini, širini, višini in v času. Čas tu ne nastopa nič drugače kot ostale običajne prostorske razsežnosti, le pri merjenju razdalj v prostoru-času, ga malo drugače obravnavamo. Seveda si štirih razsežnosti ne moremo predstavljati hkrati, lahko pa si zamislimo, kako bi izgledal svet, če bi takšne sposobnosti imeli. Običajne predmete našega trirazsežnega sveta bi videli kot štiridimenzionalne predmete v prostoru-času. To bi nam omogočalo, da bi človeka od njegovega rojstva do njegove smrti videl kot en sam štirirazsežen predmet.
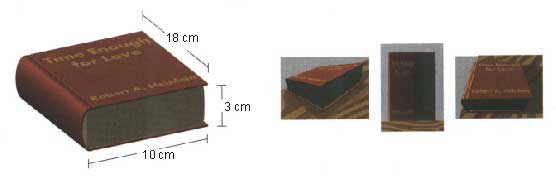
Če gledamo na naš svet kot odslikavo prostora-časa, potem ni več tako težko razumeti ugotovitev relativnosti, da različni opazovalci izmerijo različne vrednosti za časovne ali pa prostorske intervale. Poglejmo si preprosto trirazsežno analogijo. Vzemimo knjigo in prosimo več oseb, da jo natančno premeri. Seveda bodo vsi namerili enako širino, višino in dolžino knjige. Če pa istim ljudem izročimo samo različne dvorazsežne fotografije te knjige, in jih prepričamo, da verno posnemajo realnost, se bodo lahko v neskončnost prepirali, katera slika je prava. V vsakdanjem svetu zaznavamo le tri razsežnosti in prepričani smo, da naše zaznave verno odražajo realnost. Ampak prostor-čas ima štiri razsežnosti. Kot lahko naredimo različne dvorazsežne fotografije trirazsežne knjige, tako se tudi meritve intervalov prostora in časa v posameznih trirazsežnih opazovalnih sistemih razlikujejo, čeprav vsi opazovalci gledajo en in isti prostor-čas. Čeprav se prostor in čas za posamezne opazovalce razlikujeta, je prostor-čas za vse enak.
Diagrami prostora-časa
Zamisli si, da voziš avto po ravni cesti od doma do trgovine. Recimo, da ob 8:00 odpelješ izpred domače hiše in pospešiš do hitrosti 50 km/h. S to hitrostjo voziš, dokler ne zagledaš na semaforju pred seboj rdeče luči. Takrat začneš zavirati; ustaviš se tik pred semaforjem in čakaš na zeleno luč. Ko se ta pojavi ponovno pospešiš na 50 km/h, nakar s to hitrostjo ne voziš do trgovine, kjer ob 8:10 ponovno počasi ustaviš in parkiraš. Kako bi tvoja pot izgledala v prostoru-času?
Če bi lahko videli vse štiri razsežnosti prostora-časa, bi tvojo pot videli kot podobo avtomobila, ki je raztegnjena čez 10 minut časovne razsežnosti. Čeprav si vseh štirih razsežnosti ne moremo zamisliti naenkrat, je primer s potjo avtomobila po ravni cesti dovolj enostaven, saj si potoval le vzdolž ene same prostorske razsežnosti. Svojo pot skozi prostor-čas lahko tako predstaviš z diagramom, ki ima na eni osi razdaljo, za katero si se oddaljil od doma, na drugi osi pa čas, ki je potekel, odkar si odpeljal od doma. Takšen graf se imenuje diagram prostora-časa.
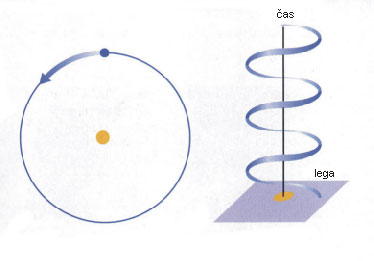
Pot avtomobila oz. kateregakoli predmeta skozi štirazsežni prostor-čas se imenuje svetovnica, vsaka točka vzdolž svetovnice pa predstavlja posamezni dogodek. Začetni dogodek je torej, ko ob 8:00 zapustiš dom, in končni dogodek, ko ob 8:10 prispeš do trgovine. Pomembne lastnosti vsake svetovnice so:
- Svetovnica vsakega predmeta, ki miruje, je navpična oz. vzporedna s časovno osjo. Predmet se namreč ne premika v prostoru, ampak le v času.
- Svetovnica predmeta, ki se giblje s konstantno hitrostjo je ravna, a nagnjena. Bolj ko je svetovnica nagnjena, hitreje se predmet giblje.
- Svetovnica objekta, ki se pospešuje, je ukrivljena. Če se hitrost povečuje, je svetovnica ukrivljena proti prostorski osi, če pa se hitrost zmanjšuje, je svetovnica zmeraj bolj navpična.
V relativnosti se prostorske razdalje običajno izražajo s časovnimi enotami (ali pa obratno časovne s prostorskimi), tako npr. razdalje izražamo v svetlobnih sekundah ali svetlobnih letih. V tem primeru so svetovnice svetlobe v diagramu prostora-časa vedno nagnjene za 45°.
Poskušajmo si sedaj s pomočjo diagramov prostora-časa razjasniti relativnost prostora in časa posamično. Zamislimo si, da se s Tino gibljeta en proti drugemu s konstantno hitrostjo 0,9c. Seveda bosta narisala vsak svoj diagram prostora časa, kjer bo vertikalna črta, ki predstavlja mirovanje, enkrat ustrezala Tini, drugič pa tebi. Posebna teorija relativnosti napove, da boš ti videl Tinin čas teči počasneje, Tina pa tvojega. Vendar, kot smo že ugotovili, tu ni nobenega protislovja. Nihče od vaju nima vpogleda v celotni štirirazsežni prostor-čas, ampak ga gledata vsak skozi svojo trirazsežno perspektivo. Prav zaradi tega vidiš tudi Tinin čas teči počasneje in ona tvojega.
Ukrivljenost prostora-časa
Do sedaj smo govorili le o ravnem prostoru-času, kot že vemo, pa je prostor-čas lahko tudi ukrivljen. Čeprav si zlahka predstavljamo ukrivljenost dvorazsežne ploskve, si ukrivljenosti prostora-časa nikakor ne moremo predstavljati. Kaj torej pomeni, da je prostor-čas ukrivljen?
Odgovor se skriva v geometriji. Poglejmo si najpreprostejši primer dvorazsežne ukrivljene ploskve, ki jo lahko ponazorimo kar s površino Zemlje. Vsi vemo, da česa takega, kot je ravna črta na krogelni površini Zemlje ne moremo narisati. Najkrajša in najbolj ravna črta, ki jo lahko narišemo, je vedno del velikega kroga – kroga katerega središče leži v Zemljinem središču. Primer takšnega velikega kroga je ekvator, pa tudi vsak poldnevnik, medtem ko vzporedniki niso takšne črte, ker njihovo središče ni v središču Zemlje. Če bi radi našli najkrajšo pot med dvema krajema na Zemljini površini, moramo preprosto slediti poti velikega kroga. Najkrajša pot med New Yorkom in Pekingom tako ni sledenje vzporedniku na 40° severne širine, ampak let čez severni pol.
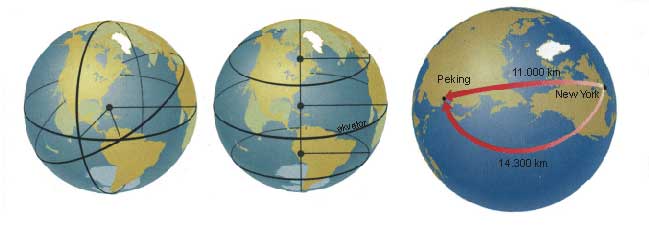
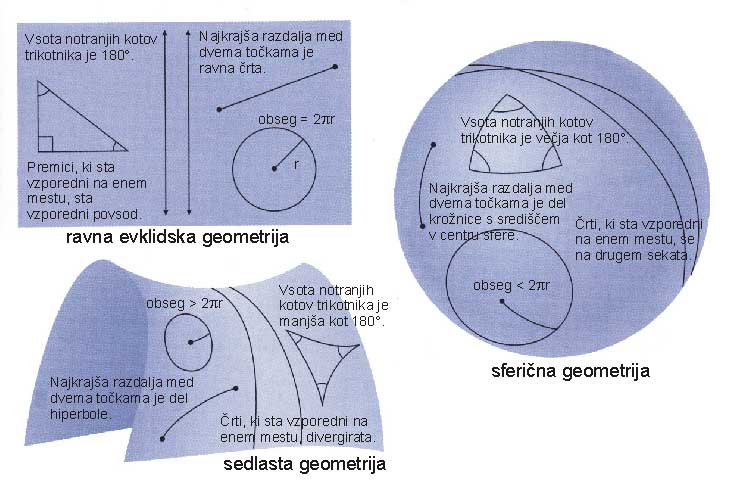
Primerjajmo sedaj geometrijo na Zemljinem površju z geometrijo na ravni ploskvi. Na ravni ploskvi se dve vzporedni premici ne bosta nikoli sekali in obseg kroga vedno znaša natanko 2πr. Na površini sfere ti dve ugotovitvi ne veljata več. Tudi najbolj ravne črte, ki jih lahko narišemo na površini sfere, se bodo vedno križale, čeprav so lahko na določenih krajih vzporedne ena drugi. Podobno je tudi obseg kroga narisanega na sferi manjši kot 2πr.
Če te ugotovitve posplošimo tudi na večrazsežne prostore, lahko rečemo, da ima prostor ali prostor-čas ravno geometrijo, če v njem držijo pravila za ravno oz. evklidsko geometrijo. V njem mora biti obseg kroga vedno enak 2πr. Če je v nekem prostoru obseg kroga manjši kot 2πr, za takšen prostor pravimo, da ima sferično geometrijo. Če je obseg kroga večji kot 2πr, pa ima tak prostor sedlasto ali hiperbolično geometrijo, ki si jo najlaže ponazorimo z obliko sedla. Resnična ukrivljenost prostora-časa je pravzaprav mešanica vseh treh tipov geometrije.
“Ravne” črte v ukrivljenem prostoru-času
O geometriji prostora-časa vemo že zelo veliko, če znamo ugotoviti, ali se predmet giblje skozi prostor-čas po najkrajši poti. Ker si ne moremo predstavljati niti časovnega dela prostora-časa niti njegove ukrivljenosti, nas zanima, kako lahko torej ugotovimo, če se predmet res giblje po najkrajši poti?
Einstein si je pri iskanju odgovora na to vprašanje pomagal z načelom ekvivalentnosti. Po njem lahko občutek teže enakovredno pripišemo pospeševanju ali gravitacijskem polju. Podobno lahko občutek breztežnosti interpretiramo kot prosto padanje ali pa kot gibanje s konstantno hitrostjo daleč stran od gravitacijskih polj. Ker pomeni potovati s konstantno hitrostjo tudi potovati po ravni črti, je Einstein sklepal, da se vsi predmeti, ki zaradi kateregakoli vzroka čutijo breztežnost, gibljejo po najbolj “ravni” oz. najkrajši poti skozi prostor-čas. Torej, če prosto lebdiš, potem sledi tvoja svetovnica najkrajši poti skozi prostor-čas. Če čutiš težo, potem nisi na najkrajši možni poti. Na ta način smo dobili zelo zanesljivo metodo, kako raziskovati geometrijo prostora-časa. Spomnimo se, da so vse orbite pravzaprav svetovnice prostopadajočih predmetov. Po načelu ekvivalentnosti predstavljajo vse orbite poti predmetov, ki se gibljejo skozi prostor-časa po najkrajši možni poti. Oblike in hitrosti posameznih orbit tako odkrivajo geometrijo prostora-časa, kar nam omogoča tudi povsem nov pogled na gravitacijo.
Gravitacija kot ukrivljenost prostora-časa
Snov pove prostoru, kako naj se ukrivi, in prostor pove snovi, kako naj se giblje. (John Wheeler)
Newtonov gravitacijski zakon pravi, da iz vsakega masnega telesa izvira gravitacijska privlačnost do vsakega drugega masnega telesa, ne glede na to, kako daleč je. Vendar se že kmalu izkaže, da je to delovanje na daljavo zelo skrivnostno, če ga pogledamo bolj podrobno. Kako lahko npr. Zemlja čuti Sončevo privlačnost in zakaj kroži okoli njega? Tudi Newtona samega so mučila takšna vprašanja, saj je le nekaj let zatem, ko je leta 1687 objavil svoj gravitacijski zakon zapisal: “Da lahko eno telo učinkuje na drugo preko vakuuma, in da se tako prenaša sila, je zame tako velik absurd, da verjamem, kako nihče, ki je sposoben razumnega mišljenja, na to ne more pristati.”
Einsteinova splošna teorija relativnosti ukinja idejo o delovanju sil na daljavo. Trdi namreč, da telo (recimo planet Zemlja) ne čuti nobenih skrivnostnih sil, ampak le sledi najkrajši poti skozi prostor-čas, ker je prostor-čas v okolici Sonca je ukrivljen. Z drugimi besedami povedano: kar zaznamo kot gravitacijo, je le posledica ukrivljenosti prostora-časa.

Štiridimenzionalnega prostora-časa si ne moremo predstavljati, vendar si lahko marsikaj predstavimo tudi z dvodimenzionalno analogijo. Za primerjamo si prostor-čas zamislimo kot prožno ponjavo, ki naj nima na površini nobenega trenja, kot ga tudi nima prazni prostor. Sonce ponazorimo s težko maso, ki jo postavimo na sredo ponjave, ki ponjavo ukrivi v lijaku podobno obliko. Predmeti, ki se prosto gibljejo, sledijo potem, ki so tako ravne, kot je le mogoče na ukrivljeni ponjavi. Masa v sredini teh predmetov ne privlači, ne komunicira z njimi ali kako drugače nanje ne vpliva. Predmeti spreminjajo smer svojega gibanja le zato, ker je ponjava ukrivljena. Po Einsteinovi teoriji planeti krožijo okoli Sonca, ker masa Sonca ukrivi prostor tako, da je kroženje najbolj naravni način gibanja. Če povzamemo: masa povzroči, da se prostor-čas ukrivi, ukrivljenost prostora-časa pa določa poti prosto gibajočim se masam.
Analogija ponjave je zelo uporabna, vendar se moramo zavedati nekaj pomembnih omejitev:
- Ponjava predstavlja vesolje, zato nima nobenega pomena dejstvo, da masi položimo na vesolje. Bolje bi bilo, da bi si predstavljali maso znotraj ponjave.
- S ponjavo si lahko predstavljamo orbite le v dveh dimenzijah. Lahko si predstavljamo npr. kako različni planeti krožijo v različnih razdaljah od Sonca in da imajo eni bolj eliptično orbito kot drugi, ne moremo si pa predstaviti dejstva, da vsi planeti ne krožijo v isti ravnini.
- Analogija s ponjavo ne prikazuje časovnega dela prostora-časa. Za zaključene orbite se zdi, da se po enem obhodu vrnejo nazaj v isto točko, vendar se v resničnem prostoru-času predmeti ne morejo vrniti nazaj v isto točko, ker se neprestano gibljejo naprej v času. Z vsakim obhodom Sonca se npr. Zemlja vrne na isto mesto v prostoru relativno na Sonce, a v času je za eno leto drugje.
Jakost gravitacije in ukrivljenost prostora-časa
Bolj ko se prostor-čas ukrivi, močnejša je gravitacija. Po analogiji s ponjavo lahko ugotovimo, da lahko povečamo ukrivljenost prostora-časa na dva osnovna načina. Večja ko je masa, večja je ukrivljenost na enaki razdalji od središča mase. Sonce tako bolj ukrivi prostor-čas kot npr. planet in Zemlja bolj kot npr. Mesec. Za predmet dane mase, pa je ukrivljenost prostora-časa na njegovi površini tem večja, čim gostejši je. Če bi Sonce stisnili na velikost zvezde tipa bela pritlikavka, to ne bi vplivalo na ukrivljenost prostora-časa daleč stran od Sonca, tik ob Sončevi površini pa bi se ukrivljenost močno povečala. Gravitacija je tako na površini bele pritlikavke veliko večja, kot je na površini Sonca.

Če s stiskanjem Sonca nadaljujemo do vedno večjih gostot, bo postajal prostor-čas na površini vedno bolj ukrivljen. V končni fazi bi naredili v prostoru času jamo brez dna, ki ji rečemo tudi črna luknja. Iz črne luknje ne more pobegniti prav nič, zato je vse, kar pade vanjo za nas za vedno izgubljeno. Meja, ki predstavlja točko od koder naprej ni več povratka, se imenuje horizont dogodkov, ker dogodki, ki se zgodijo onkraj tega horizonta, nimajo nikakršnega vpliva na naš opazljivi svet. Črna luknja je res luknja v opazljivem vesolju.
Gravitacijska dilatacija časa
Ker že vemo, da je gravitacija posledica ukrivljenosti prostora-časa, nas ne sme presenetiti, da gravitacija vpliva tudi na tek časa in ne samo na ukrivljenost prostora. Vpliv gravitacije na čas si lahko ogledamo preko vplivov pospešenega gibanja, potem pa na ugotovitve apliciramo načelo ekvivalentnosti.
Zamisli si, da s Tino lebdita vsak na svojem koncu iste vesoljske ladje. Oba imata sinhronizirani uri, ki vsako sekundo močno zasvetita. Ker oba prosto lebdita in se relativno drug na drugega ne gibljeta, sta oba v istem opazovalnem sistemu, zato bosta videla obe uri teči in utripati usklajeno oz. z enako frekvenco. Sedaj pa si zamisli, da prižgeš raketne motorje in ladja začne pospeševati s tabo na kljunu in Tino na repu. Ker se ladja pospešuje, s Tino nista več v breztežnosti. Pospeševanje pa povzroči še eno pomembno spremembo, ki je mogoče že bolj pomembna, kot je občutek teže. Spomnimo se, da so opazovalci, ki se gibljejo z različnimi relativnimi hitrostmi, v različnih opazovalnih sistemih. Ko se ladja pospešuje, se njena hitrost, glede na zunanjega prostolebdečega opazovalca, konstantno povečuje, kar pomeni, da s Tino neprestano spreminjata opazovalne sisteme. Bliski s tvoje ure potrebujejo nekaj časa, da prepotujejo od kljuna do repa ladje. Do trenutka, ko te uspe doseči utrip iz Tinine ure (ali utrip tvoje ure doseže Tino), sta tvoj in Tinin opazovalni sistem že spremenjena, glede na stanje takrat, ko je bil utrip oddan.
Ker si ti na kljunu pospešujoče se ladje, te bo spreminjanje opazovalnih sistemov zmeraj neslo stran od mesta, kjer je bil vsak od pulzov s Tinine ure oddan. Zato bo potrebovala svetloba vsakega od utripov njene ure malo več časa, da te doseže, kot bi potrebovala, če se ladja ne bi pospeševala. Posledica tega je, da vidiš, kako pulzi s Tinine ure ne prihajajo v razmiku 1 sekunde, kot jih Tinina ura oddaja, ampak v razmiku, ki je malo večji. Tinino uro vidiš tako teči malo počasneje, kot svojo. Sklepal boš torej, da teče čas na repu ladje počasneje.
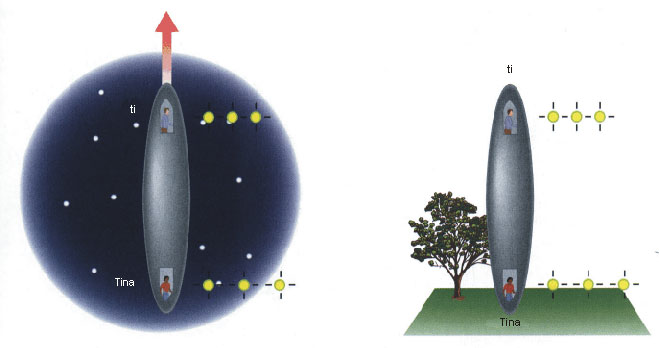
Tina pa z repa pospešujoče se ladje nasprotno vidi, kako jo spreminjanje opazovalnih sistemov nese proti točkam, od koder izvirajo svetlobni bliski tvoje ure. Zato bo potreboval vsak blisk s tvoje ure manj časa, da bo dosegel Tino, kot bi potreboval, če se ladja ne bi pospeševala, zato bo Tina videla, kako si utripi tvoje ure sledijo v razmikih, ki so malo manjši od 1 sekunde. Tvojo uro bo videla utripati malo hitreje kot svojo, zato bo sklepala, da teče čas na kljunu ladje hitreje. S Tino se torej strinjata, da teče čas hitreje na sprednjem koncu ladje in počasneje na zadnjem. Večje, kot je pospeševanje ladje, večja bo razlika med hitrostjo teka časa na obeh koncih ladje.
Sedaj pa uporabimo še načelo ekvivalentnosti, ki pravi, da moramo priti do enakih ugotovitev za ladjo, ki miruje v gravitacijskem polju, kot smo jih dobili za ladjo, ki je pospeševala med gibanjem skozi prostor. Če bi tako ladja mirovala na planetu, bi morali po isti logiki opaziti, da čas teče hitreje na kljunu in počasneje na repu. To pomeni, da mora čas teči počasneje na nižjih višinah kot na večjih višinah v gravitacijskem polju. Ta pojav nosi ime gravitacijska dilatacija časa.
Močnejša kot je gravitacija – in s tem povezana večja ukrivljenost prostora-časa -, večji bo faktor za katerega teče čas počasneje. Čas teče počasneje na površini Sonca, kot teče na površini Zemlje, in počasneje na površini bele pritlikavke kot na površini Sonca. Skrajni primer pa je seveda črna luknja. Opazovalec, ki gleda v smeri črne luknje bo namreč videl, kako se na horizontu dogodkov čas ustavi. Če bi razmestili ure na različnih oddaljenostih od črne luknje, bi opazili, da ure bližje horizonta dogodkov tečejo počasneje, na samem horizontu pa bi jih videli kot zamrznjene.
Geometrija vesolja
Če pogledamo skozi okno izgleda, kot da je površina Zemlje nekje ravna, na drugih koncih pa nagubana s hribi in dolinami. Ko pa pogledamo Zemljo kot celoto npr. iz vesolja, pa nam postane jasno, da ima površina zemlje obliko dokaj pravilne sfere. Na podoben način, vendar z dvema dodatnima dimenzijama, ima tudi štiridimenzionalni prostor-čas celotnega vesolja določeno geometrijsko obliko, ki jo določa masa v njem. Geometrija je lahko ravna, sferična ali pa sedlasta.
V geometriji je ravnina neskončno velika. Prav tako je neskončna sedlasto ukrivljena (hiperbolična) površina. Na podoben način bi bilo vesolje neskončno, če bi imelo ravno ali sedlasto geometrijo. V tem primeru ne bi imelo ne središča ne roba. Če pa bi bila geometrija vesolja sferična, bi bil prostor-čas končen, kot je končno velika površina Zemlje, vendar vesolje še zmeraj ne bi imelo ne središča ne roba. Prav tako kot lahko letimo ali plujemo okoli Zemlje brez bojazni, da bi padli čez rob, bi lahko večno potovali po vesolju in nikoli ne bi naleteli na rob. In tako kot na površini Zemlje ni nobene privilegirane točke, ki bi jo lahko imenovali središče – Ljubljana ni nič manj v središču kot npr. London – tudi vesolje nima središča.
Razrešitev paradoksa dvojčkov
Zamisli si dvojčka, od katerih eden ostane na Zemlji, drugi pa se poda na pot z zelo hitro raketo do bližnje zvezde in nazaj. V miselnem poskusu 13 (glej članek o posebni teoriji relativnosti) smo napovedali, da se bo dvojček, ki je potoval po vesolju, manj postaral, kot njegov brat, ki je ostal na Zemlji. Kaj ne bi lahko z istimi argumenti tudi potujoči brat trdil, da je pravzaprav on miroval, na popotovanje stran in nazaj glede nanj pa se je odpravila Zemlja z drugim bratom na njej? Kaj ne bi moral biti po tej logiki brat na Zemlji tisti, ki se je manj postaral? Z vprašanjema smo odprli v t. i. paradoks dvojčkov. Poskušajmo ga razrešiti!
Zamisli si, da lebdita skupaj s Tino v breztežnosti vsak v svoji vesoljski ladji eden ob drugemu in sinhronizirata svoje ure. Medtem ko ti ostaneš v breztežnosti, Tina vklopi na svoji ladji motorje in se pospešeno odpelje malo stran, nato pa z vzvratnimi motorji zavre in se ustavi. Potem se obrne in na enak način vrne na mesto ob tebi od koder se je podala na pot. Iz tvojega opazovalnega sistema vidiš, da Tinine ure bijejo počasneje kot tvoje. Ob njenem povratku tako pričakuješ, da je zanjo poteklo manj časa, kot zate. In kako vidi dogajanje Tina? Ali vidi tudi ona dogajanje natanko tako kot ti?
S Tino se lahko neskončno časa prepirata, kdo se zares giblje, vendar se okoli nečesa vseeno morata strinjati: med popotovanjem si ti ostal v breztežnosti, medtem ko je Tina ob pospeševanju čutila težo, ki jo je pritisnila k tlom njene vesoljske ladje. Tina si lahko svojo težo razlaga na dva različna načina. Lahko se strinja s tabo, da je bila ona tista, katere ladja se je pospeševala. Ker pa vemo, da teče čas počasneje v pospešeni vesoljski ladji, se bo tako Tina morala strinjati, da so njene ure tekle počasneje kot tvoje. Lahko pa ubere drugačno pot in trdi, da je čutila težo zato, ker so se morali motorji na njeni ladji upirati gravitacijskemu polju, v katerem je bila pri miru, medtem ko si ti v njem prosto padal. Ker pa vemo, da teče čas v gravitacijskem polju počasneje, se mora tudi v tem primeru s Tino strinjati, da tečejo njene ure počasneje od tvojih. Ne glede na to, kako s Tino interpretirata dogajanje, je rezultat enak: za Tino poteče med popotovanjem manj časa.
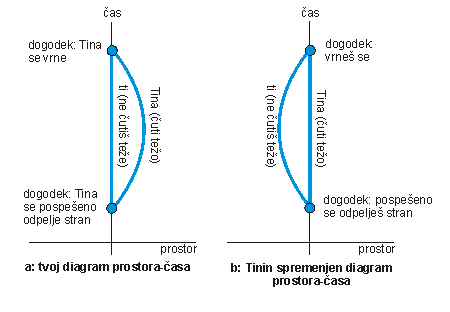
Zgornja slika a kaže diagram našega poskusa v prostoru-času. S Tino sta se oba gibala med istima točkama v prostoru-času – med začetkom in koncem Tinine poti – vendar je tvoja pot med obema dogodkoma krajša kot Tinina. Ker smo že ugotovili, da je za Tino poteklo manj časa, lahko potegnemo presenetljiv zaključek o naravi teka časa: med katerima koli dogodkoma v prostor-času, poteče več časa, ko potujemo po krajši poti. Največ časa porabimo za pot med dvema dogodkoma v prostoru-času, če sledimo čimbolj ravni poti – to je poti, na kateri ne občutimo teže oz. pospeševanja.
Kaj pa če Tina trdi, da miruje in pripiše svojo težo gravitacijskemu polju? V tem primeru bi narisala diagram poti v prostoru-času kot ga prikazuje slika b, na kateri izgleda, da imaš pravzaprav ti daljšo pot skozi prostor-čas. Po pravilu, da teče čas počasneje na daljših poteh, bi morale tako teči počasneje tvoje ure, kar je v nasprotju z našimi prejšnjimi ugotovitvami. Vendar je to protislovje le navidezno. Če hoče Tina trditi, da je čutila gravitacijo, mora iz tega nujno tudi sklepati, da je prostor-čas v njeni okolici ukrivljen, kar pa pomeni, da svojega diagrama poti ne more izrisati na raven kos papirja.
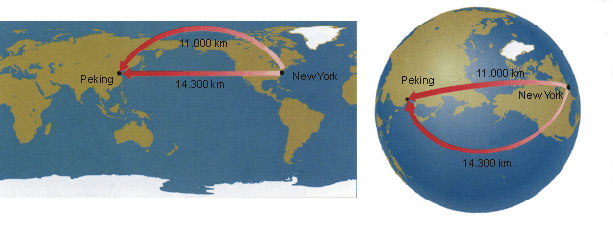
Tinina težava je analogna težavi, s katero se sreča pilot, ki načrtuje polet npr. iz New Yorka v Peking na ravnem zemljevidu Zemlje. Na ravnem zemljevidu izgleda, da je pilot izbral najbolj ravno pot, vendar je takšna izbira le navidezna. Najkrajša pot med obema točkama je v resnici zakrivljena pot, ki gre skoraj preko severnega pola. Ravni zemljevid Zemlje popači realnost, ker je resnična geometrija Zemljinega površja sferična. Tako kot popačenja na zemljevidu Zemlje ne spremenijo resničnih razdalj med mesti, tudi naša izbira, kako bomo narisali diagram poti v prostoru-času ne spremeni realnosti prostora-časa. Razrešitev paradoksa dvojčkov je torej v ugotovitvi, da oba brata nista občutila enakih okoliščin, zato njuni poti nista zamenljivi. Brat, ki je potoval do bližnje zvezde in nazaj, mora imeti bolj zavito svetovnico (oz. črto, ki povezuje njegove lege v prostoru-času) kot brat, ki je ostal doma. Za brata, ki je ostal na Zemlji, je zato res poteklo več časa in brat, ki je potoval, se je res manj postaral.
Eksperimentalne potrditve splošne teorije relativnosti
Iz načela ekvivalentnosti smo z analogijami razvili nekaj idej splošne relativnosti. Seveda lahko tem idejam verjamemo le, če so podprte s poskusi in opazovanji. Kot posebna teorija relativnosti, je bila tudi splošna teorija soočena z veliko preizkusi, ki jih je vse zelo uspešno prestala.
Čudaška Merkurjeva orbita
Prvi test, ki ga je opravila splošna relativnost, se je nanašal na opazovanje Merkurjeve orbite. Newtonovi zakoni so predvidevali, da se mora Merkurjeva orbita počasi spreminjati (precesirati) zaradi vpliva drugih planetov. Natančna opazovanja Merkurja v 19. stoletju so precesijo potrdila in ugotovila, da traja en precesijski približno 20.000 let. Vendar pa izračuni s pomočjo Newtonovih enačb nikakor niso uspeli napovedati točno takšne precesije. Čeprav so bile razlike majhne, so še bolj natančna opazovanja potrdila, da so odstopanje od napovedi Newtonovih enačb res prisotna.
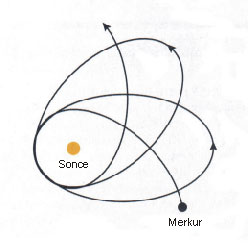
Einstein se je teh odstopanj zavedal in že od leta 1907 naprej, ko je prišel na idejo načela ekvivalentnosti, upal, da bo uspel ta odstopanja pojasniti. Ko mu je novembra 1915 končno uspelo, ga je to tako razveselilo, da bil naslednje 3 dni od razburjenja povsem nesposoben za kakršnokoli delo. Kasneje je ta dogodek poimenoval za najvišjo točko v njegovem znanstvenem življenju.
Einstein je pokazal, da pride do neujemanja med opazovanji in klasično Newtonovo napovedjo, ker Newtonov gravitacijski zakon predpostavlja absolutni čas in ravni prostor. V realnosti pa je tek časa odvisen od okoliščin in prostor v bližini Sonca, kjer leži Merkurjeva orbita, je že nezanemarljivo ukrivljen. Enačbe splošne relativnosti upoštevajo deformacije prostora-časa in napovejo Merkurjevo orbito, ki se natančno ujema z opazovanji.
Gravitacijsko lečenje
Einsteinove ugotovitve lahko preverimo tudi tako, da opazujemo poti svetlobnih žarkov skozi vesolje. Ker potuje svetloba zmeraj z isto hitrostjo (nikoli ne pospešuje ali zavira) mora potovati vedno po najbolj ravni poti, kot je le mogoče. Če je prostor ukrivljen, bo seveda tudi svetloba potovala po ukrivljeni poti.
Zamislimo, si, da lahko izmerimo kot med dvema zvezdama, ko njuna svetloba potuje mimo Sonca. Ukrivljenost prostora v Sončevi bližini prisili svetlobo, ki potuje bližje Soncu, da se njena pot bolj zakrivi kot svetloba z zvezde, ki potuje bolj stran od Sonca. Njuna medsebojna kotna razdalja bo tako manjša, kot bi bila, če Sonca ne bi bilo v bližini, ker lahko preverimo, če bi izmerili kot ponoči, ko Sonca ni v bližini. Ta pojav so prvič opazovali med Sončevim mrkom leta 1919. Ta drugi veliki uspeh splošne teorije relativnosti je botroval Einsteinovi slavi po vsem svetu.
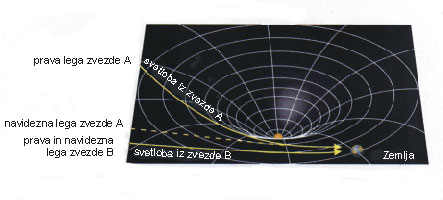
Še bolj spektakularen pa je pojav, če opazujemo oddaljeno zvezdo ali galaksijo, pred katero je v smeri proti Zemlji objekt z zelo veliko maso.
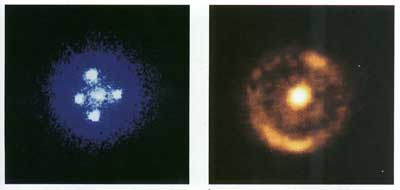
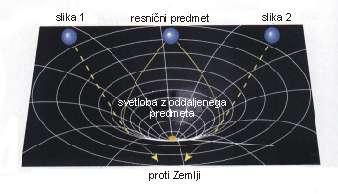
Masa tega objekta ukrivi prostor v okolici, kar spremeni tudi smer svetlobi, ko potuje mimo. Svetlobni žarki, ki so prej potovali v različne smeri, se lahko ukrivijo in vsi prispejo na Zemljo, kar deformira sliko zvezde ali galaksije, ki žarke oddaja. Glede na geometrijo prostora-časa med objektom in Zemljo, se lahko slika objekta deformira v križe, obroče ali pa se le podvoji ali potroji.Takšne deformacije se imenujejo gravitacijsko lečenje po analogiji z lomljenjem žarkom pri prehodu skozi steklene leče.
Upočasnitev časa
Napoved o gravitacijski dilataciji časa lahko preverimo s primerjavo natančnih ur, ki tečejo v področjih z različnim gravitacijskim poljem. Že v Zemljini relativno šibki gravitaciji so poskusi z urami na različnih nadmorskih višinah pokazali, da ure višje res tečejo hitreje. Razlika je zelo majhna – v človeškem življenju bi razlika znesla le nekaj milijonink sekunde -, vendar se natančno ujema z napovedi splošne relativnosti.
Zanimivo je, da je še laže, kot primerjati tek časa na različnih koncih Zemlje, primerjati čas na Zemlji s tekom časa na Soncu ali drugih zvezdah. Ker plini v zvezdah absorbirajo ali pa oddajajo svetlobo točno določenih frekvenc, nam lahko posamezne črte v spektru služijo kot naravne atomske ure. Recimo, da v Zemeljskem laboratoriju izmerimo, ga določen plin oddaja svetlobo s frekvenco 500 trilijonov nihajev na sekundo. Če je ta plin prisoten tudi na Soncu, bo tudi tam oddajal svetlobo s to isto frekvenco. Splošna relativnost napoveduje, da teče čas na Soncu za malenkost počasneje kot čas na Zemlji; 1 sekunda na Soncu traja dlje kot 1 sekunda na Zemlji oz. sekunda na Zemlji je krajša od sekunde na Soncu. V eni zemeljski sekundi bomo videli tako manj kot 500 trilijonov nihajev plina na Soncu. Ker manjša frekvenca pomeni večjo ali bolj rdečo valovno dolžino, pravimo, da so spektralne črte redeče premaknjene. Opozorimo še, da gravitacijski rdeči premik, ki nastane zaradi upočasnjevanja časa v gravitacijskem polju, nima nič skupnega z Dopplerjevim rdečim premikom, ki ga opazimo zaradi gibanja objektov. Gravitacijski rdeči premik so izmerili za spektralne črte svetlobe iz Sonca in drugih zvezd in meritve so se vedno ujemale z napovedmi splošne relativnosti.
Iskanje gravitacijskih valov
Če se ukrivljenost prostora-časa nenadoma nekje spremeni, ima to lahko posledice tudi za oddaljene dele vesolja. Nenadna eksplozija zvezde ima podoben učinek, kot če vržemo kamen v jezero. Pojavijo se valovi, ki se širijo stran od točke, kamor smo vrgli kamen. Če se dve masivni zvezdi vrtita druga okoli druge, tudi povzročata nastajanje valovanja. Einstein je valovanje te vrste imenoval gravitacijski valovi. Po obnašanju so podobni valovom svetlobe (nimajo mase in potujejo s svetlobno hitrostjo), le da so veliko bolj šibki. Deformacije prostora, ki jih nosijo gravitacijski valovi, bi povzročile nenadno stiskanje in razširjanje objektov, skozi katere se bi te valovi gibali. V načelu bi lahko zaznali gravitacijske valove tako, da bi pazljivo opazovali dolžine izbranih objektov, vendar še nikomur ni uspelo izmeriti spremembe dolžine objekta, ki bi jo lahko pripisal gravitacijskim valovom, čeprav je kar nekaj raziskovalnih skupin to že poskušalo.
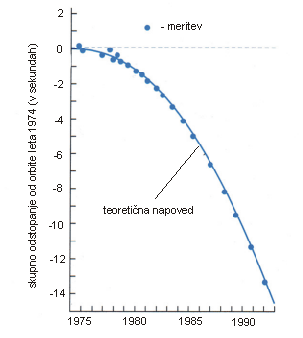
Čeprav neposrednega dokaza gravitacijskih valov še nimamo, pa imamo zelo dober posredni dokaz, ki sta ga leta 1974 našla astronoma Russell Hulse in Joseph Taylor. Opazovala sta sistem dveh zelo masivnih nevtronskih zvezd, od katerih je bila ena pulzar, ki sta se vrteli ena okoli druge z zelo veliko hitrostjo. Splošna relativnost napoveduje, da bi moral takšen sistem oddajati kar nekaj energije v obliki gravitacijskih valov. Če sistem res oddaja energijo tudi v takšni obliki, se mora razdalja med obema zvezdama počasi manjšati. Večletna opazovanja so pokazala, da se orbitalna perioda zvezd zmanjšuje natanko tako, kot napoveduje splošna relativnost, kar je zelo močan argument, da gravitacijski valovi res obstajajo.
Nekaj knjig o splošni teoriji relativnosti:
- Strnad, Janez : “Na pot k Schwarzschildu”, Ljubljana : DMFA, 1991 – 52 str. (Enostaven uvod v splošno teorijo relativnosti, a le uvod in nič več.)
- Ellis, George F.R. & Williams, Ruth M. : “Flat and curved space-times”, Oxford : Oxford Univ. Press, 1988 – 350 str. (Zelo dober uvodni učbenik relativnosti, ki ne zahteva znanja višje matematike.)
- Weinberg, Steven : “Gravitation and cosmology : principles and applications of the general theory of relativity”, New York [etc.] : John Wiley, 1972 – 657 str. (Čeprav nekoliko stara, še vedno zelo cenjena in uporabna knjiga.)
- Ohanian, Hans C. : “Gravitation and spacetime” , New York : W. W. Norton, 1976, – 461 str. (Zelo opevana knjiga zaradi “pedagoškega pristopa”.)
- Misner, Charles W. , Thorne, Kip S. , Wheeler, John Archibald : “Gravitation”, New York : W. H. Freeman and Company, 1995, cop. 1973, 1279 – str. (Ponatis monumentalne knjige – skoraj 1300 strani! – iz sedemdesetih let.)
- Wald, Robert M. :”General relativity”, Chicago, London : The University of Chicago Press, 1984 – 491 str.
- Callahan, James J. : “The geometry of spacetime : an introduction to special and general relativity”, New York [etc.] : Springer, cop. 2000 – 451 str.
- Dirac, Paul Adrien Maurice :”General theory of relativity” , Princeton : Princeton Univ. Press, 1996 – 69 str. (Kljub novi letnici je to ponatis stare knjige enega od velikih fizikov 20. st. – le uvod v teorijo relativnosti.)
Zgornji tekst je priredba poglavja o relativnosti iz knjige The Cosmic Perspective, 1999.