Marsikdo od nogometnih navdušencev se bo spomnil prostega strela, ki ga je izvedel Brazilec Roberto Carlos na močnem meddržavnem turnirju poleti leta 1997 v Franciji. Strel je bil dosojen na razdalji približno 30 metrov od francoskih vrat, rahlo na desni strani. Carlos je brcnil žogo tako močno na desno, da je obšla živi zid za več kot meter. Na ponovljenem posnetku je bilo videti pobiralca žog nekaj metrov stran od vrat, kako je sklonil glavo, misleč da je v nevarnosti. Potem je žoga, kot po čudežu, zavila v levo in zadela desni kot vrat, na veliko presenečenje vratarja, igralcev in gledalcev.
Menda je Carlos prosti strel iz podobnega položaja zavzeto treniral. Intuitivno je vedel, kako bo žoga zavila, če jo zadene na določen način. Najbrž pa ni vedel prav nič o fizikalnem ozadju tega pojava.
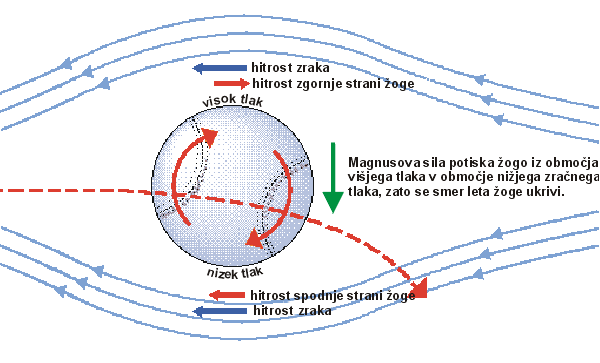
Ko je lord Rayleigh opisoval, zakaj se spreminja smer letečih objektov, ki se hkrati vrtijo okrog svoje osi, je prvo razlago tega pojava pripisal nemškemu fiziku Gustavu Magnusu leta 1852. Magnusa je v resnici zanimalo, zakaj se na stran odklonijo izstrelki, vendar je mogoče njegovo razlago prav tako dobro uporabiti za primer, ko je izstrelek žoga, saj je osnovni mehanizem praktično enak. Vzemimo, da se žoga vrti okrog osi, ki je pravokotna na tok zraka mimo nje. Zrak potuje okoli žoge hitreje tam, kjer se površina žoge giblje v isti smeri kot tok zraka. V skladu z Bernoullijevo enačbo je na tistem mestu pritisk na žogo manjši kot na drugi strani, kjer je hitrost zraka glede na središče žoge manjša in zato lokalni pritisk večji. Zaradi razlike pritiskov se pojavi prečna sila, ki deluje pravokotno na smer zračnega toka in osi vrtenja ter povzroči, da žoga v letu zavije, t.i. Magnusov efekt.
Pa poglejmo, kakšne sile delujejo na žogo pri dobro izvedenem prostem strelu. Pri hitrosti žoge okrog 100 km/h, ki se vrti z 8 do 10 obrati na sekundo, znaša Magnusova sila okrog 3.5 N. Pravila zahtevajo, da žoga za profesionalni nogomet tehta od 410 do 450 gramov, tako da žoga prečno na smer leta pospešuje z 8 metri na sekundo v sekundi. Ker bo 30 metrov do gola preletela približno v eni sekundi, pomeni, da bo Magnusova sila premaknila žogo okrog 4 metre iz začetne smeri. Dovolj, da spravi v škripce prav vsakega vratarja.
Poleg Magnusove sile deluje na žogo še sila zračnega upora, v smeri, ki je nasprotna smeri gibanja. V grobem je zaviranje sorazmerno s kvadratom hitrosti žoge, odvisno pa je še od koeficienta zračnega upora, na katerega vpliva način gibanja zraka okoli žoge. Pri majhnih hitrostih so tokovnice okrog žoge lepo urejene in gladke, zrak se nekoliko vrtinči le za zadnjim delom žoge, zračni tok je pretežno laminaren. Pri velikih hitrostih se zrak okrog žoge močno vrtinči, zračni tok je turbulenten. V takih razmerah prepotuje plast zraka, ki se giblje tik nad površino, precej večjo razdaljo preden se odlepi od žoge, kot če je tok laminaren. Zato je pri majhnih hitrostih žoge koeficient zračnega upora precej večji kot pri velikih hitrostih. Sprememba iz enega načina zaviranja v drugega je precej ostra. Hitrost, pri kateri se način obtoka bistveno spremeni, je odvisna še od hrapavosti površine žoge. če leti žoga tako hitro, da se zrak okrog nje močno vrtinči, je njeno zaviranje relativno majhno, na račun manjšega koeficienta zračnega upora. Hitra žoga je torej dvakrat nevarna za vratarja. Ne le da se giblje z veliko hitrostjo, tudi zavira manj, kot bi pričakovali. Zdi se, da najboljši vratarji intuitivno razumejo več fizike, kot bi si mislili.
Leta 1976 je Peter Bearman s sodelavci iz Imperial Collegea v Londonu izpeljal serijo poskusov z žogicami za golf. Prepričali so se, da je Magnusova sila večja, če se žogica pri isti hitrosti vrti hitreje, pa še, da se pri isti hitrosti vrtenja Magnusova sila zmanjša, če se poveča hitrost žogice. Žoga torej na koncu svoje poti zavija najmočneje, ker je njena hitrost najmanjša, če vzamemo, da se hitrost vrtenja med letom bistveno ne zmanjša.
Kako vse to pojasni prosti strel Roberta Carlosa? Čeprav ne moremo biti popolnoma gotovi, se je najbrž zgodilo takole: Carlos je udaril po žogi z zunanjo stranjo leve noge, tako da se je zavrtela v nasprotni smeri urinega kazalca, gledano od zgoraj navzdol. Bile so suhe vremenske razmere, tako da se je žoga močno zavrtela, približno z 10 obrati v sekundi. Udarec z zunanjo stranjo noge je žogi hkrati podelil veliko hitrost, verjetno več kot 30 metrov na sekundo. Tok zraka okrog površine žoge je bil turbulenten, tako da je bila sila zračnega upora relativno majhna. Nekje vzdolž poti žoge, recimo po 10 metrih (približno položaj živega zidu) se je hitrost tako zmanjšala, da je postal zračni tok okrog žoge urejen, laminaren. Sila zračnega upora je tedaj močno narasla in še bolj zavrla žogo, hkrati pa se je povečala prečna Magnusova sila. Bolj ko se je žoga zaustavljala, močneje je zavijala proti golu, dokler se ni znašla v mreži – na veliko zadovoljstvo fizikov med navijači.
Raziskave v nogometu se ne omejujejo več le na študij obnašanja žoge v letu. Raziskovalce zanima, kako nogometaši v resnici udarijo po žogi. Stanley Plagenhof z univerze Massachusetts v ZDA je študiral kinematiko brcanja. Drugi raziskovalci, recimo Elizabeth Roberts in sodelavci z univerze Wisconsin, so se ukvarjali z dinamično analizo brcanja, ki upošteva tudi sile na delu. Dokopali so se do nekaterih zanimivih rezultatov, vendar je ostalo odprtih še mnogo vprašanj. En od glavnih problemov takih raziskav so natančne meritve človeškega gibanja, delno tudi zato, ker je le-to tako nepredvidljivo. Bistven napredek na področju znanosti o športu je omogočil razvoj zmogljivih računalnikov. S pomočjo računalniško podprtih znanstvenih metod je danes mogoče s precejšnjo natančnostjo meriti in spremljati človeško gibanje.
Takeshi Asai in Takao Akatsuka ter njuni sodelavci z univerze Yamagata na Japonskem so uporabili računalniški pristop, združen z bolj konvencionalnimi metodami dinamične analize za simulacijo nogometnega udarca po žogi. Ustvarili so t.i. virtualnega nogometaša s širokim razponom sposobnosti, ki lahko v virtualnem prostoru in času posnema nogometno igro otrok in začetnikov, pa tudi profesionalnih igralcev. Izdelovalce športne opreme, recimo korporacijo ASICS, ki spozorira projekt Yamagata, precej zanima tak znanstveni pristop k fenomenu nogometnega udarca. Upajo, da bodo rezultate lahko uporabili pri oblikovanju bolj varne in bolj učinkovite športne opreme, ki bi jo bilo mogoče izdelovati hitreje in bolj ekonomično v primerjavi z današnjimi izdelki.
Gibanje igralcev so raziskovalci spremljali s pomočjo hitrega videa s 4500 posnetki na sekundo, udarec po žogi pa so študirali s pomočjo metode končnih elementov. Začetni poskusi so pokazali tisto, kar večina nogometašev že ve: če udariš žogo neposredno s konico noge v smeri, ki gre skozi težišče, odleti žoga v isti smeri naprej. Če je udarec nekoliko drugačen, necentralen, se žoga zavrti in v letu zavija. Eksperiment je pokazal, da je rotacija (spin), ki jo dobi žoga, močno odvisna od trenja med žogo in obuvalom ter od razdalje med centrom in točko, kjer obuvalo zadene žogo. Raziskovalci so analizirali različne vrste udarcev po žogi. Ugotovili so, da se žoga vrti hitreje, večje ko je trenje, in (ali) bolj ko je udarec necentralen. Opazili so še dva zanimiva pojava. Pri velikih razdaljah od centra je udarna noga v stiku z žogo krajši čas in na manjši površini. Posledica tega je, da se zmanjša oboje, hitrost in spin žoge. Za dosego maksimalne hitrosti vrtenja obstaja torej najbolj primerno mesto, kjer je treba zadeti žogo: udarec preblizu ali predaleč od centra bo žogi podelil manjši spin. Druga zanimivost je, da v primeru, ko ni trenja med obuvalom in žogo, le-ta še vedno dobi nekaj spina, če je udarec izven centra. Čeprav v tem primeru ni sile trenja, ki bi delovala vzporedno z obodom žoge (ker je koeficient trenja nič), se žoga vseeno deformira proti centru, kar povzroči silo, ki zavrti žogo okrog težišča. Tudi v deževnem vremenu, ko je trenje med obuvalom in žogo majhno, je torej mogoče zavrteti žogo.
Kljub nekaterim pomanjkljivostim raziskovalci pravijo, da vsebuje njihov model najpomembnejše elemente, ki vplivajo na kakovost nogometnega udarca. V prihodnje nameravajo študirati, kako se pri udarcu obnesejo različne vrste nogometnih čevljev. Medtem pri ASICS-u kombinirajo rezultate, dobljene pri simulaciji, z dognanji iz biomehanike, fiziologije in fizike materialov, da bi izboljšali nogometno obutev. Vendar pa je še vedno nogometaš tisti, od katerega je največ odvisno, tehnologija sama brez njegove spretnosti ne zaleže kaj dosti.
Kaj se torej lahko naučimo od Roberta Carlosa? Če udariš žogo tako močno, da je zračni tok v njeni okolici turbulenten, bo koeficient zračnega upora majhen in žoga bo zares poletela. Če hočeš, da žoga v letu zavije, jo moraš z nogo zadeti izven centra, da se hkrati zavrti. Če je zunaj mokro, je žogo še zmerom mogoče zavrteti, vendar je to ob suhih dnevih veliko lažje. Žoga prične močno zavijati, ko preide zračni tok okoli nje v laminarni režim. Treba je le še vaditi, da se to zgodi na pravem mestu, na primer takoj zatem, ko žoga prileti mimo živega zidu.
S svojim prostim strelom je Roberto Carlos 4. junija 1997 v Lyonu iztržil neodločen izid za svojo reprezentanco. Na veliko razočaranje vseh Brazilcev pa mu predstave ni uspelo ponoviti naslednje leto, na zaključnem srečanju svetovnega prvenstva, ko so se Brazilci znova pomerili s Francozi. Njegov morebitni zadetek v finalu, dosežen na podoben način, bi le potrdil veljavnost fizikalnih zakonov, ki se jim ne moremo izogniti niti v nogometu. S stališča fizika ne bi bil torej nič posebej razburljivega. Vse kaj drugega pa bi veljalo za nogometnega navdušenca v Braziliji, kar priča, da se čar nogometne igre skriva povsem drugje kot v fizikalnih zakonih, ki pa se jim hote ali nehote (verjetno pa nevede) ne morejo izogniti niti najboljši nogometaši sveta.
V nadaljnje branje:
- T. Asai, T. Akatsuka in S. Haake 1998, The physics of football (Phys. World 6, 25-27)
- C.B.Daish 1972, The Physics of Ball Games (The English University Press, London)
- S. J. Haake (ed) 1996, The Engineering of Sport (A A Balkema, Rotterdam)
- R D Mehta 1985, Aerodynamics of sports balls (Ann. Rev. Fluid Mech. 17, 151-189)
Matjaž Žitnik, kvarkadabra.net – številka 5, junij 2000.