V Kvarkadabrinem fokusu predstavljamo delo skupine slovenskih fizikov z Instituta Jožef Stefan in FMF Univerze v Ljubljani, ki so uspeli z optično pinceto manipulirati topološke defekte v tekočih kristalih in “tkati” splete. Delo je bilo objavljeno v reviji Science, ima pa precejšen potencial za uporabo na različnih drugih področjih fizike. Prvega avtorja članka, Uroša Tkalca z IJS in Max Planckovega Instituta v Göttingenu smo prosili za odgovore na standardna vprašanja Kvarkadabrinega fokusa.
Kaj? (Referenca)
Reconfigurable Knots and Links in Chiral Nematic Colloids. Science 1 July 2011: Vol. 333, no. 6038, pp. 62-65.
Kdo? (Avtorji)
Uroš Tkalec (IJS in MPI-DS), Miha Ravnik (Univ. Oxford in FMF, Univ. Ljubljana), Simon Čopar (FMF), Slobodan Žumer (FMF in IJS), Igor Muševič (IJS in FMF).
Kje? (“slovenska”, “evropska” ali “svetovna” raziskava?)
Gre za domačo raziskavo petih slovenskih raziskovalcev. Ideja se mi je porodila v času doktorskega študija pri prof. dr. Igorju Muševiču, tako da sem celotno eksperimentalno delo opravil na Institutu Jožef Stefan. Pri teoretični obravnavi rezultatov sta mi pomagala dr. Miha Ravnik in Simon Čopar pod vodstvom prof. dr. Slobodana Žumra. Zaključno fazo priprave članka sem opravil kot podoktorski sodelavec Max Planckovega instituta za dinamiko in samo-organizacijo v Göttingenu.
Zakaj?(Kako bi izsledke razložili svoji babici, dedku, teti, stricu…?)
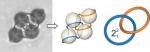Povsem na kratko z veliko strokovnega žargona: v članku obravnavamo kontrolirano oblikovanje vozlov in spletov iz topoloških defektnih linij, ki nastanejo v koloidni mešanici tekočega kristala in mikroskopsko majhnih steklenih kroglic. Naj nekoliko podrobneje pojasnim. Tekoči kristali so tiste tekočine, ki se skrivajo v LCD zaslonih telefonov, računalnikov in televizij. Ob pomoči elektronike znajo ustvariti sliko. V članku smo proučevali kombinacijo tekočega kristala in primešanih mikrometrskih delcev. To ni čisto običajna tekočina, čeprav teče kot voda ali olje. A po drugi strani se obnaša kot elastična snov. Vzrok za to dvojnost je, da so tekočekristalne molekule orientirane (v našem primeru so to urejene toge palčke z dolžino 2 nanometrov). Ko zapremo tanko plast takšnega materiala med dve stekelci, se podolgovate molekule tekočega kristala poravnajo vzporedno s površino stekla. Površina dodanih kroglic nasprotno vsiljuje v svoji bližini pravokotno urejanje tekočekristalnih molekul. Zaradi tega konflikta nastanejo topološki defekti – območja v tekočini, kjer urejenost molekul ni dobro definirana. Te lahko prepoznamo pod mikroskopom kot ozke črne zanke, ki obdajajo koloidne kroglice.
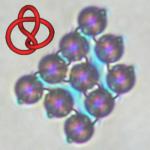Zaradi omenjenih elastičnih napetosti smo lahko ustvarili prepletene koloidne strukture v tekočih kristalih. Pri tkanju teh prepletenih vzorcev, kjer so kroglice povezane z zavozlanimi in/ali spletenimi defektnimi zankami sem uporabljal optično pinceto. To je eksperimentalna naprava, ki s pomočjo močno fokusiranega laserskega snopa omogoča da »primemo« posamezne defektne obročke in z njimi povlečemo skupaj več sosednjih kroglic. Defektna linija se namreč obnaša kot elastična vrvica, ki jo je mogoče raztegovati in preoblikovati s svetlobo iz laserja. Če zvišamo intenziteto laserskega snopa, lahko del takšne defektne linije lokalno stalimo oziroma efektivno »prerežemo« in nato povežemo z zanko okrog bližnje kroglice. Po izklopu laserja se tekoči kristal v deformiranem območju zaradi nenadnega lokalnega padca temperature hipoma uredi v eno izmed možnih metastabilnih konfiguracij. V kolikor se omejimo na štiri sosednje delce, imamo zgolj tri različne možnosti za prostorsko razporeditev dveh sosednjih defektnih linij – bodisi tvorita križišče bodisi sta mimobežni v dveh pravokotnih smereh. Poenostavljeno rečeno, z uporabo laserske svetlobe smo lahko ustvarili topološke objekte – vozle in splete.
Z uporabo orodij iz matematične teorije vozlov je mogoče te objekte tudi prepoznati in ustrezno klasificirati. V pričujočem članku nam je uspelo matematično pojasniti vse opažene tipe vozlov in spletov ter obenem napovedati katere izmed njih lahko sestavimo na koloidnih strukturah izbrane velikosti. Za ilustracijo, z zgolj 16 kroglicami je mogoče izdelati okrog 80 topološko različnih tipov vozlov in zank, ki se pojavijo v skoraj 20.000 različnih konfiguracijah. Velja omeniti, da gre v tem primeru za eno izmed redkih eksperimentalnih realizacij matematične teorije vozlov v fiziki nasploh. Doslej objavljeni prispevki s tega področja namreč zgolj opisujejo bodisi posredno identifikacijo posameznih vozlov v biokemijskem okolju bodisi teoretično oblikovanje najpreprostejših vozlov v različnih fizikalnih poljih. V vseh teh primerih je množica eksperimentalno dostopnih vozlov omejena na le nekaj osnovnih primerov, sam postopek vozlanja pa je večinoma zelo zapleten in slabo kontroliran. Naše delo te dosežke vsebinsko dopolnjuje in konceptualno nadgrajuje. Kot prvi smo namreč pokazali, da je mogoče poljubne vozle in splete kontrolirano splesti in ponovno preplesti iz topoloških defektnih zank na mikroskopskem nivoju. Predstavljen način tkanja tudi omogoča izdelavo vozlov »po naročilu« na urejenih mrežah koloidnih delcev in neposredno računalniško podprto analizo spletenih struktur. Nenazadnje je naša strategija vozlanja univerzalna, saj se jo lahko z ustrezno uporabo zunanjih polj praktično uporabi na vrsti drugih fizikalnih sistemov: od polimerov, makromolekul, DNK, do vrtincev v tekočinah in superprevodnikih. Razen tega vidimo v našem sistemu tudi potencialni praktični pomen. Vozle in splete v tekočih kristalih bi namreč lahko uporabili za vezavo in izdelavo t.i. fotonske snovi, ki bi uravnavala tok svetlobe v prihajajočih optičnih mikrovezjih.
Kako? (Kje se je najbolj zatikalo?)
Raziskave so potekale dobri 2 leti. Zgodba se ni začela z idejo o vozlih, ampak je nastajala postopoma. Prvotni cilj je bilo sestavljanje dvodimenzionalnih prepletenih koloidnih kristalov, ki so bili teoretično napovedani v simulacijah dr. Mihe Ravnika, vendar teh rezultatov v homogeno urejenem tekočekristalnem polju ni bilo mogoče eksperimentalno realizirati. Ključni korak v pravo smer je bil zasuk enega izmed stekelc za 90°. S tem enostavnim posegom v geometrijo tekočekristalne celice se je odprl nov svet prepletenih koloidnih struktur, ki so spontano nastajale že med samim polnjenjem celice. Sledilo je sistematično sestavljanje majhnih koloidnih skupkov z optično pinceto, ki je potekalo relativno enostavno, saj smo imeli s tem v laboratoriju že precej izkušenj. Kmalu sem opazil, da se število prepletenih zank od primera do primera spreminja, prav tako pa so lahko bile posamezne zanke spletene na več različnih načinov. To je vodilo do prvega soočenja z vozli in napornega študija matematične teorije vozlov. Ker v to raziskavo nismo vključili nobenega matematika, je bil napredek relativno počasen.
Razumevanje topologije spletenih zank se je izboljšalo, ko sva s kolegom Ravnikom začela uporabljati program za 3D risanje vozlov, ki sva ga kupila na svetovnem spletu za manj kot 10 EUR. Sledilo je preverjanje vseh možnih kombinacij na urejenih pravokotnih mrežah koloidnih delcev, kjer smo hitro naleteli na programerske in teoretične omejitve obravnavanega sistema. K sreči se je izkazalo, da je mogoče poljubne vozle in splete sestaviti s permutacijami treh osnovnih vzorcev, njihovo število pa je naraščalo praktično eksponentno z velikostjo sistema. Pri teh zaključnih analizah mi je bil v veliko pomoč mladi fizik Simon Čopar, ki se je s svojim izjemnim matematičnim in programerskim znanjem izkazal kot odličen sogovornik pri razvozlavanju številnih ugank. Veliko zaslug za končni uspeh gre pripisati tudi mojemu mentorju, prof. Muševiču, ki mi je omogočil dovolj svobode pri raziskovanju in ne nazadnje tudi prof. Žumru, ki nas je s svojimi bogatimi izkušnjami velikokrat usmeril na pravo pot.
Članek je bil po oddaji v uredništvo revije Science izjemno dobro ocenjen s strani recenzentov in praktično sprejet v objavo brez vsebinskih sprememb v manj kot dveh mesecih. Ob objavi je delo odmevalo tudi izven strokovne javnosti, tako doma kot po svetu, o čemer pričajo številni zapisi v tiskanih in elektronskih medijih. Zanimanje za vsebino teh raziskav niti ni tako presenetljivo, saj se s preprostimi vozli pogosto srečujemo tudi v vsakdanjem življenju, na primer pri zavezovanju čevljev ali kravate, kompleksnejši vozli pa se uporabljajo pri jadranju, plezanju, ribolovu in tkanju preprog. Kite, vozle in splete občudujemo tudi v raznih pleteninah, vzbujajo nam občutek urejenosti in naravnosti, zato še dandanes pogosto navdihujejo umetnike pri ustvarjanju zapletenih geometrijskih vzorcev, izdelavi nakita in oblikovanju arhitekturnih dekoracij.
Kam? (Naslednja velika stvar na vašem področju?)
Rezultati tega dela odpirajo številne možnosti za izdelavo vozlov in spletov na mikroskopskem nivoju – namesto defektnih linij v tekočem kristalu lahko uporabimo polimere, DNK ali biološka vlakna, morebiti celo eksotična spinska stanja v novih kovinskih materialih. Zanimivo bi bilo raziskati interakcijo holografsko ustvarjenih vozlov v optičnih vrtincih laserske svetlobe s tekočim kristalom. Določeni obeti se kažejo tudi na področju boljšega razumevanja in kontroliranja celičnih procesov, saj denimo pri prepisu DNK podobne topološke operacije izvajajo nekateri posebni encimi. Ne nazadnje pa omogoča to odkritje tudi gradnjo prilagodljivih in topološko zahtevnih arhitektur v tekočem kristalu, ki bi jih lahko v prihodnosti uporabljali za uravnavanje toka svetlobnih informacij po optičnih mikrovezjih.
(copyright pravice za slike pripadajo AAAS/Science)
